吉林省四平市伊通县2018-2019学年七年级下学期期末考试试卷
试卷更新日期:2020-05-18 类型:期末考试
一、选择题
-
1. 如图,点E在BC的延长线上,则下列条件中,能判定AD平行于BC的是( )
 A、∠1=∠2 B、∠3=∠4 C、∠D+∠DAB=180° D、∠B=∠DCE2. 如图,在一次活动中,位于 处的七年一班准备前往相距 的 处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( )
A、∠1=∠2 B、∠3=∠4 C、∠D+∠DAB=180° D、∠B=∠DCE2. 如图,在一次活动中,位于 处的七年一班准备前往相距 的 处与七年二班会合,若用方向和距离描述七年二班相对于七年一班的位置,可以描述为( ) A、南偏西40°,3km B、南偏西50°,3km C、北偏东40°,3km D、北偏东50°,3km3. 等于( )A、±4 B、4 C、﹣4 D、±24. 下列各组数值是二元一次方程2x﹣y=4的解的是( )A、 B、 C、 D、5. 已知a>b,下列不等式变形不正确的是( )A、a+2>b+2 B、a﹣2>b﹣2 C、2a>2b D、2﹣a>2﹣b6. 某中学为了解学生的视力情况,需要抽取部分学生进行调查,下列抽取方法中最合适的是( )A、随机抽取一部分男生 B、随机抽取一个班级的学生 C、随机抽取一个年级的学生 D、在各个年级中,每班各随机抽取20名学生
A、南偏西40°,3km B、南偏西50°,3km C、北偏东40°,3km D、北偏东50°,3km3. 等于( )A、±4 B、4 C、﹣4 D、±24. 下列各组数值是二元一次方程2x﹣y=4的解的是( )A、 B、 C、 D、5. 已知a>b,下列不等式变形不正确的是( )A、a+2>b+2 B、a﹣2>b﹣2 C、2a>2b D、2﹣a>2﹣b6. 某中学为了解学生的视力情况,需要抽取部分学生进行调查,下列抽取方法中最合适的是( )A、随机抽取一部分男生 B、随机抽取一个班级的学生 C、随机抽取一个年级的学生 D、在各个年级中,每班各随机抽取20名学生二、填空题
-
7. 计算: ( + )= .8. 如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,如果∠COE=40°,则∠AOD等于度.
 9. 如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为 .
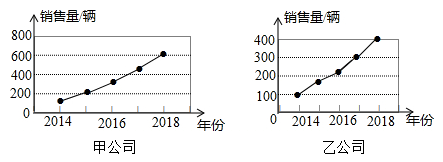
9. 如图,若在象棋盘上建立平面直角坐标系xOy,使“帥”的坐标为(﹣1,﹣2),“馬”的坐标为(2,﹣2),则“兵”的坐标为 . 10. 方程组 的解为 .11. x的 与5的和不大于3,用不等式表示为12. 甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是公司(填“甲”或“乙”).
10. 方程组 的解为 .11. x的 与5的和不大于3,用不等式表示为12. 甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是公司(填“甲”或“乙”).
 13. 某家具厂有22名工人,每名工人每天可加工3张桌子或10把椅子,1张桌子与4把椅子配成一套,现要求工人每天做的桌子和椅子完整配套而没有剩余,若设安排x名工人加工桌子,y名工人加工椅子,则列出的方程组为 .14. 请写出不等式﹣ x+2≥0的一个正整数解(写出一个即可).
13. 某家具厂有22名工人,每名工人每天可加工3张桌子或10把椅子,1张桌子与4把椅子配成一套,现要求工人每天做的桌子和椅子完整配套而没有剩余,若设安排x名工人加工桌子,y名工人加工椅子,则列出的方程组为 .14. 请写出不等式﹣ x+2≥0的一个正整数解(写出一个即可).三、综合题
-
15. 计算:16. 解方程组 .17. 解不等式组:
请结合题意填空,完成本题的解答:
(1)、解不等式①,得 ,(2)、解不等式②,得 ,(3)、把不等式①和②的解集在数轴上表示出来; (4)、原不等式组的解集为.18. 请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.
(4)、原不等式组的解集为.18. 请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.
解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
19. 如图,在平面直角坐标系中,半径为1的圆从原点出发沿x轴正方向滚动一周,圆上一点由原点O到达点O′,圆心也从点A到达点A′. (1)、点O′的坐标为 , 点A′的坐标为;(2)、若点P是圆在滚动过程中圆心经过的某一位置,求以点P,点O,点O′为顶点的三角形的面积.20. 为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题:
(1)、点O′的坐标为 , 点A′的坐标为;(2)、若点P是圆在滚动过程中圆心经过的某一位置,求以点P,点O,点O′为顶点的三角形的面积.20. 为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题: (1)、样本容量为 , 频数分布直方图中a=;(2)、扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;(3)、若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?21. 如图,已知∠A=90°+x°,∠B=90°﹣x°,∠CED=90°,4∠C﹣∠D=30°,射线EF∥AC.
(1)、样本容量为 , 频数分布直方图中a=;(2)、扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;(3)、若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?21. 如图,已知∠A=90°+x°,∠B=90°﹣x°,∠CED=90°,4∠C﹣∠D=30°,射线EF∥AC. (1)、判断射线EF与BD的位置关系,并说明理由;(2)、求∠C,∠D的度数.22. 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟,请问小华家离学校多远?23. 如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).
(1)、判断射线EF与BD的位置关系,并说明理由;(2)、求∠C,∠D的度数.22. 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟,请问小华家离学校多远?23. 如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b). (1)、顶点B的坐标为 , 顶点D的坐标为(用a或b表示);(2)、如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;(3)、在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,
(1)、顶点B的坐标为 , 顶点D的坐标为(用a或b表示);(2)、如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;(3)、在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,这次平移可以看成是先将长方形ABCD向右平移个单位长度,再向下平移个单位长度的两次平移;
(4)、若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.24. 在解方程组或求代数式的值时,可以用整体代入或整体求值的方法,化难为易.(1)解方程组 ;(2)已知 ,求x+y+z的值解:(1)把②代入①得:x+2×1=3.解得:x=1.
把x=1代入②得:y=0.
所以方程组的解为 ,(2)①×2得:8x+6y+4z=20.③
②﹣③得:x+y+z=5.
(1)、(类比迁移)
若 ,则x+2y+3z= .(2)、解方程组(3)、(实际应用)打折前,买39件A商品,21件B商品用了1080元.打折后,买52件A商品,28件B商品用了1152元,比不打折少花了多少钱?