浙江省温州市2020届九年级下学期数学质量检测试卷
试卷更新日期:2020-05-15 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. 2020的相反数为( )A、 -2020 B、 C、±2020 D、20202. 已知 的半径为 ,图心 到直线 的距离为 ,则直线 与 的位置关系为 ( )A、相交 B、相切 C、相离 D、无法确定3. 下列运算正确的是( )A、 B、 C、 D、4. 下列水平放置的几何体的主视图是圆的是(A、
 B、
B、 C、
C、 D、
D、 5. 一元一次不等式 的解集在数轴上表示为( )A、
5. 一元一次不等式 的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 6. 如图,为测量一根与地面垂直的旗杆 的高度,在距离旗杆底端 10米的 处测得旗杆顶端 的仰角 ,则旗杆 的高度为( )
6. 如图,为测量一根与地面垂直的旗杆 的高度,在距离旗杆底端 10米的 处测得旗杆顶端 的仰角 ,则旗杆 的高度为( )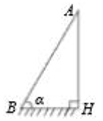 A、 米 B、 米 C、 米 D、 米7. 设 .则 在两个相邻整数之间,那么这两个整数是( )A、1和2 B、2和3 C、3和4 D、4和58. 某商店对一种商品进行促销,促销方式:若购买不超过10件,按每件 元付款:若一次性购买10件以上,超出部分按每件 元付款.小明购买了14件付款90元;小聪购买了19件付款115元,则 , 的值为( )A、 B、 C、 D、9. 将一个边长为4的正方形 分割成如图所示的9部分,其中 , , , 全等, , , , 也全等,中间小正方形 的面积与 面积相等,且 是以 为底的等腰三角形,则 的面积为( )
A、 米 B、 米 C、 米 D、 米7. 设 .则 在两个相邻整数之间,那么这两个整数是( )A、1和2 B、2和3 C、3和4 D、4和58. 某商店对一种商品进行促销,促销方式:若购买不超过10件,按每件 元付款:若一次性购买10件以上,超出部分按每件 元付款.小明购买了14件付款90元;小聪购买了19件付款115元,则 , 的值为( )A、 B、 C、 D、9. 将一个边长为4的正方形 分割成如图所示的9部分,其中 , , , 全等, , , , 也全等,中间小正方形 的面积与 面积相等,且 是以 为底的等腰三角形,则 的面积为( ) A、2 B、 C、 D、10. 如图,在 中, 是 的内切圆,连结 , ,则图中阴影部分的面积之和为( )
A、2 B、 C、 D、10. 如图,在 中, 是 的内切圆,连结 , ,则图中阴影部分的面积之和为( ) A、 B、 C、12 D、14
A、 B、 C、12 D、14二、填空题(本题有6小题,每小题5分,共30分)
-
11. 计算:12. 某校为了解本校学生参加课外兴趣小组的情况,从全体学生中随机抽取了50名学生进行调查,并将调查结果绘制成统计表(如下),已知该校学生总数为1000人,由此可以估计参加体育类兴趣小组的学生为
兴趣小组
美术类
音乐类
科技类
体育类
人数
8
10
12
20
13. 一个圆锥的主视图为边长等于 的等边三角形,则这个圆锥的侧面积为 . 14. 如图, 和 是 的切线,点 和点 是切点, 是 的直径,连结 ,已知 , 则
14. 如图, 和 是 的切线,点 和点 是切点, 是 的直径,连结 ,已知 , 则 15. 如图,在平面直角坐标系中,菱形 的顶点 在坐标原点,边 在 轴的负半轴上, ,顶点 的坐标为 .反比例数 的图象与菱形对角线 AO 交于点 ,连结 ,当 轴时, 的值是
15. 如图,在平面直角坐标系中,菱形 的顶点 在坐标原点,边 在 轴的负半轴上, ,顶点 的坐标为 .反比例数 的图象与菱形对角线 AO 交于点 ,连结 ,当 轴时, 的值是 16. 如图,在矩形 中, 分别是 的中点, 分别在 , 上, 且 ,连结 ,则 与 重叠部分六边形 的周长为
16. 如图,在矩形 中, 分别是 的中点, 分别在 , 上, 且 ,连结 ,则 与 重叠部分六边形 的周长为
三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
-
17.(1)、计算: ;(2)、已知 ,求 与 的比.18. 如图是由5个边长为1的正方体叠放而成的一个几何体,请画出这个几何体的三视图.(用铅笔描黑)
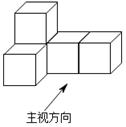
 19. 如图,在 中,点 在 的延长线上,且 .连结 ,交 于点 ,
19. 如图,在 中,点 在 的延长线上,且 .连结 ,交 于点 , (1)、求证: :(2)、若 ,求 的长,20. 一栋家属楼高 ,小王在楼顶 处测得对面楼房 的顶端 的俯角是30°;小王下来 到 (即 ),在 处测得楼房 的底端 的俯角是45°;求楼房 的高.(直接用无理数表示,无需求近似值)
(1)、求证: :(2)、若 ,求 的长,20. 一栋家属楼高 ,小王在楼顶 处测得对面楼房 的顶端 的俯角是30°;小王下来 到 (即 ),在 处测得楼房 的底端 的俯角是45°;求楼房 的高.(直接用无理数表示,无需求近似值) 21. 如图,在 中, ,以 为直径的 交 于点 .延长 交 于点 , 是 的切线,作 .垂足为 .
21. 如图,在 中, ,以 为直径的 交 于点 .延长 交 于点 , 是 的切线,作 .垂足为 . (1)、求证: ;(2)、若 ,求 的长.22. 如图,抛物线 上有一点 , 的横坐标为1,过 作 轴,与抛物线的另一个交点为 ,且 ,作 轴,垂足为 ,抛物线与 轴正半轴交于点 ,连结 与 交于点 .
(1)、求证: ;(2)、若 ,求 的长.22. 如图,抛物线 上有一点 , 的横坐标为1,过 作 轴,与抛物线的另一个交点为 ,且 ,作 轴,垂足为 ,抛物线与 轴正半轴交于点 ,连结 与 交于点 . (1)、当 时,①求点 的坐标:②求 的面积:(2)、当 是以 为腰的等腰三角形时,求 的值.23. 某校一面墙 前有一块空地,校方准备用长 的栅栏( )围成一个一面靠墙的长方形花围,再将长方形 分割成六块(如图所示),已知 , , ,设 .
(1)、当 时,①求点 的坐标:②求 的面积:(2)、当 是以 为腰的等腰三角形时,求 的值.23. 某校一面墙 前有一块空地,校方准备用长 的栅栏( )围成一个一面靠墙的长方形花围,再将长方形 分割成六块(如图所示),已知 , , ,设 . (1)、用含 的代数式表示:(2)、当长方形 的面积等于 时,求 的长.(3)、若在如图的甲区域种植花卉.乙区域种柏草坪,种柏花卉的成本为每平方米100元,种被草坪的成本为每平方米50元,若种植花卉与草坪的总费用超过6300元,求花围的宽 的范围.24. 如图.在 中, , , , 是 的中位线,连结 ,点 是边 上的一个动点,连结 交 于 ,交 于 .
(1)、用含 的代数式表示:(2)、当长方形 的面积等于 时,求 的长.(3)、若在如图的甲区域种植花卉.乙区域种柏草坪,种柏花卉的成本为每平方米100元,种被草坪的成本为每平方米50元,若种植花卉与草坪的总费用超过6300元,求花围的宽 的范围.24. 如图.在 中, , , , 是 的中位线,连结 ,点 是边 上的一个动点,连结 交 于 ,交 于 . (1)、当点 是 的中点时,求 的值及 的长(2)、当四边形 与四边形 的面积相等时,求 的长:(3)、如图2.以 为直径作 .
(1)、当点 是 的中点时,求 的值及 的长(2)、当四边形 与四边形 的面积相等时,求 的长:(3)、如图2.以 为直径作 .①当 正好经过点 时,求证: 是 的切线:
②当 的值满足什么条件时, 与线段 有且只有一个交点.