浙江省宁波市2020年数学中考模拟试卷（3月）
试卷更新日期：2020-05-15 类型：中考模拟
一、选择题（每小题3分，共30分）
-
1. 计算6÷（﹣3）的结果是（ ）A、﹣ B、﹣2 C、﹣3 D、﹣182. 下列图形中，是中心对称图形的是（ ）A、
B、
C、
D、
3. 分别写有数字0，﹣1，﹣2，1，3的五张卡片，除数字不同外其他均相同，从中任抽一张，那么抽到负数的概率是（ ）A、 B、 C、 D、4. 如图，是一个由3个相同的正方体组成的立体图形，则它的主视图为（ ）
A、
B、
C、
D、
5. 下列运算正确的是（ ）A、3a+2a=a5 B、a2•a3=a6 C、（a+b）（a﹣b）=a2﹣b2 D、（a+b）2=a2+b26. 如图，直线l∥m，将含有45°角的三角板ABC的直角顶点C放在直线m上，若∠1=25°，则∠2的度数为（ ）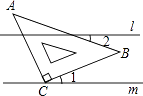
A、20° B、25° C、30° D、35°7. 在同一平面直角坐标系内，将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度，得到图象的顶点坐标是（ ）A、（﹣1，1） B、（1，﹣2） C、（2，﹣2） D、（1，﹣1）8. 下列命题是真命题是（ ）A、4的平方根是2 B、有两边和一角对应相等的两个三角形全等 C、方程x2=x的解是x=1 D、顺次连接任意四边形各边中点所得到的四边形是平行四边形9. 设二次函数y1=a（x﹣x1）（x﹣x2）（a≠0，x1≠x2）的图象与一次函数y2=dx+e（d≠0）的图象交于点（x1 ， 0），若函数y=y1+y2的图象与x轴仅有一个交点，则（ ）A、a（x1﹣x2）=d B、a（x2﹣x1）=d C、a（x1﹣x2）2=d D、a（x1+x2）2=d10. 如图，⊙O上有一个动点A和一个定点B，令线段AB的中点是点P，过点B作⊙O的切线BQ，且BQ=3，现测得 的长度是 ， 的度数是120°，若线段PQ的最大值是m，最小值是n，则mn的值是（ ）
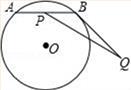A、3 B、2 C、9 D、10二、填空题（每小题4分，共24分）
-
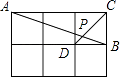
11. 18500000用科学记数法表示为 ．12. 分解因式：ax2﹣ay2= ．13. 2013年至2017年某城市居民用汽车拥有量依次为：11、13、15、19、x（单位：万辆），若这五个数的平均数为16，则x的值为.14. 如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值是 ．
15. 如图，在Rt△ABC 中，∠ACB=90°，AC=6，BC=8，点D是线段AB上的动点，M、N分别是AD、CD的中点，连接MN，当点D由点A向点B运动的过程中，线段MN所扫过的区域的面积为 ．
16. 如图，O为坐标原点，点C的坐标为（1，0），∠ACB=90°，∠B=30°，当点A在反比例函数y= 的图象上运动时，点B在函数（填函数解析式）的图象上运动．
三、解答题（本题共8小题，共66分）
-
17. 计算： × +|﹣4|﹣9×3﹣1﹣20180 ．18. 解不等式组： .19. 如图，在平行四边形ABCD中，E、F为BC上两点，且BE=CF，AF=DE，求证：
(1)、△ABF≌△DCE；(2)、四边形ABCD是矩形.20. 如图，四边形ABCD放在在平面直角坐标系中，已知AB∥CD，AD=BC，A（﹣2，0）、B（6，0）、D（0，3），反比例函数的图象经过点C．
(1)、求点C的坐标和反比例函数的解析式；(2)、将四边形ABCD向上平移2个单位后，问点B是否落在该反比例函数的图象上？21. “端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗．我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A，B，C，D表示）这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．
请根据以上信息回答：
(1)、将两幅不完整的图补充完整；
(2)、本次参加抽样调查的居民有多少人？(3)、若居民区有8000人，请估计爱吃D粽的人数．22. 如图，AB是⊙O的直径，F是⊙O外一点，过点F作FD⊥AB于点D，交弦AC于点E，且FC=FE．
(1)、求证：FC是⊙O的切线；(2)、若⊙O的半径为5，cos∠FCE= ，求弦AC的长．23. A、B两地相距150km，甲、乙两人先后从A地出发向B地行驶，甲骑摩托车匀速行驶，乙开汽车且途中速度只改变一次，如图表示的是甲、乙两人之间的距离S关于时间t的函数图象（点F的实际意义是乙开汽车到达B地），请根据图象解答下列问题：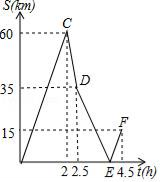
(1)、求出甲的速度；(2)、求出乙前后两次的速度，并求出点E的坐标；(3)、当甲、乙两人相距10km时，求t的值．24. 已知，如图1，O是坐标原点，抛物线y=ax2+bx+c（a≠0）经过A、B、C三点，AB⊥y轴于点A，AB=2，AO=4，OC=5，点D是线段AO上一动点，连接CD、BD．
(1)、求出抛物线的解析式；(2)、如图2，抛物线的对称轴分别交BD、CD于点E、F，当△DEF为等腰三角形时，求出点D的坐标；(3)、当∠BDC的度数最大时，请直接写出OD的长．