浙江省杭州市2020年数学中考模拟试卷（3月）

试卷更新日期：2020-05-15 类型：中考模拟

进入出卷网下载

一、选择题（共10小题，满分27分）

1. 已知某种型号的纸100张厚度约为1cm，那么这种型号的纸13亿张厚度约为（　　）

A、1.3×10⁷km B、1.3×10³km C、1.3×10²km D、1.3×10km

查看试题解析
2. 如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三种视图中面积最小的是（）

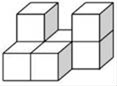A、主视图 B、俯视图 C、左视图 D、一样大

查看试题解析
3. 下面是小林做的4道作业题：（1）2ab+3ab=5ab；（2）（﹣2a）²=﹣2a²；（3）（a+b）²=a²+b²；（4）﹣2（a﹣1）=﹣2a﹣1.做对一题得2分，则他共得到（　　）

A、2分 B、4分 C、6分 D、8分

查看试题解析
4. 下列说法不正确的是（）

A、选举中，人们通常最关心的数据是众数 B、从1，2，3，4，5中随机抽取一个数，取得奇数的可能性比较大 C、甲、乙两人在相同条件下各射击10次，他们的平均成绩相同，方差分别为S_甲²=0.4，S_乙²=0.6，则甲的射击成绩较稳定 D、数据3，5，4，1，﹣2的中位数是4

查看试题解析
5. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有x名同学，根据题意，列出方程为（）

A、x（x+1）=1035 B、x（x﹣1）=1035×2 C、x（x﹣1）=1035 D、2x（x+1）=1035

查看试题解析
6. 在平面直角坐标系中，经过点（4sin45°，2cos30°）的直线，与以原点为圆心，2为半径的圆的位置关系是（）

A、相交 B、相切 C、相离 D、以上三者都有可能

查看试题解析
7. 如图，在由边长为1的小正方形组成的网格中，点A，B，C都在小正方形的顶点上.则 $cos ∠ A$ 的值为（）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $2$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{1}{2}$

查看试题解析
8. 下列说法：①平方等于其本身的数有0，±1；②3²xy³是4次单项式；③将方程= $\frac{x - 1}{0.3} - \frac{x + 2}{0.5}$ =1.2中的分母化为整数，得 $\frac{10 x - 10}{3} - \frac{10 x + 20}{5}$ =12；④平面内有4个点，过每两点画直线，可画6条.其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知：矩形ABCD中，AB=5，BC=12，点E在对角线AC上，且CE=6，动点P在矩形ABCD的四边上运动一周，则以P、E、C为顶点的等腰三角形有（　　）个.

A、5 B、6 C、7 D、8

查看试题解析
10. 如图，点M是双曲线y₁=﹣ $\frac{2}{x}$ （x＜0）上一点，直线y₂=2x+2分别与x轴、y轴交于点A，B，MC∥x轴交直线y₂于点C，MD∥y轴交直线y₂于点D，则AC•BD的值为（　　）

A、2 $\sqrt{5}$ B、5 C、 $\frac{5 \sqrt{5}}{2}$ D、不能确定

查看试题解析

二、填空题（共6小题，满分24分，每小题4分）

11. 分解因式（xy﹣1）²﹣（x+y﹣2xy）（2﹣x﹣y）= ．

查看试题解析
12. 函数y= $\frac{\sqrt{2 x + 1}}{x - 3}$ 的自变量x的取值范围是．

查看试题解析
13. 若a²+b²﹣2a+6b+10=0，则a+b= ．

查看试题解析
14. 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=（x﹣1）²﹣4，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为.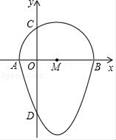

查看试题解析
15. 如图，在△ABC中，∠BAC=90°，AB=4，AC=6，点D、E分别是BC、AD的中点，AF∥BC交CE的延长线于F，则△AFC的面积为.

查看试题解析
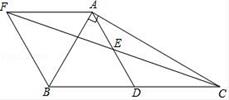16. 如图，顺次连接圆内接矩形各边的中点，得到菱形ABCD，若BD=10，DF=4，则菱形ABCD的边长为.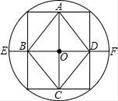

查看试题解析

三、解答题（共7小题，满分54分）

17. 先化简，再求值：（ $\frac{1}{x - 3}$ + $\frac{1}{x + 3}$ ）• $\frac{9 - 3 x}{2 x}$ ，其中x= $\sqrt{3}$ ﹣3.

查看试题解析
18. 某校九年级开展征文活动，征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个，九年级每名学生按要求都上交了一份征文，学校为了解选择各种征文主题的学生人数，随机抽取了部分征文进行了调查，根据调查结果绘制成如下两幅不完整的统计图．

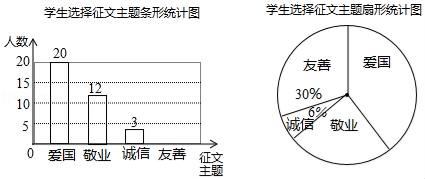(1)、求共抽取了多少名学生的征文；

(2)、将上面的条形统计图补充完整；

(3)、在扇形统计图中，选择“爱国”主题所对应的圆心角是多少；

(4)、如果该校九年级共有1200名学生，请估计选择以“友善”为主题的九年级学生有多少名．

查看试题解析
19. 在某市实施城中村改造的过程中，“旺鑫”拆迁工程队承包了一项10000m²的拆迁工程．由于准备工作充分，实际拆迁效率比原计划提高了25%，提前2天完成了任务，请解答下列问题：

(1)、求“旺鑫”拆迁工程队现在平均每天拆迁多少m²；

(2)、为了尽量减少拆迁给市民带来的不便，在拆迁工作进行了2天后，“旺鑫”拆迁工程队的领导决定加快拆迁工作，将余下的拆迁任务在5天内完成，那么“旺鑫”拆迁工程队平均每天至少再多拆迁多少m²？

查看试题解析
20. 对于一个各个数位上的数字均不为零的三位正整数n，如果它的百位数字、十位数字、个位数字是由依次增加相同的非零数字组成，则称这个三位数为“递增数”，记为D（n），把这个“递增数”的百位数字与个位数字交换位置后，得到321，即E（123）=321，规定F（n）= $\frac{E (n) - D (n)}{198}$ ，如F（123）= $\frac{321 - 123}{198}$ =1.

(1)、计算：F（159），F（246）；

(2)、若D（s）是百位数字为1的数，D（t）是个位数字为9的数，且满足
F（s）+F（t）=5，记k= $\frac{2 D (s) + D (t)}{9}$ ，求k的最大值.

查看试题解析
21. 如图，△ABC内接于⊙O，直径DE⊥AB于点F，交BC于点 M，DE的延长线与AC的延长线交于点N，连接AM.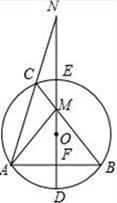

(1)、求证：AM=BM；

(2)、若AM⊥BM，DE=8，∠N=15°，求BC的长.

查看试题解析
22. 在平面直角坐标系xOy中，抛物线y=﹣x²+2mx﹣3+4m﹣m²的对称轴是直线x=1

(1)、求抛物线的表达式；

(2)、点D（n，y₁），E（3，y₂）在抛物线上，若y₁＞y₂ ，请直接写出n的取值范围；

(3)、设点M（p，q）为抛物线上的一个动点，当﹣1＜p＜2时，点M关于y轴的对称点形成的图象与直线y=kx﹣4（k≠0）有交点，求k的取值范围.

查看试题解析
23. 如图，在△ABC中，∠ACB=90°，∠ABC=30°，△CDE是等边三角形，点D在边AB上．

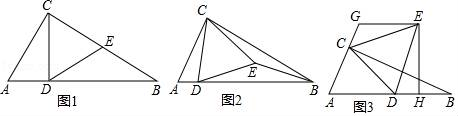(1)、如图1，当点E在边BC上时，求证DE=EB；

(2)、如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；

(3)、如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG=5CG，BH=3．求CG的长．

查看试题解析