浙江省绍兴市越城区绍初教育集团2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-05-15 类型：期中考试

进入出卷网下载

一、选择题：（本大题有10个小题，每小题3分，共30分）

1. 如图，直线a，b被直线c所截，a∥b，∠1＝60°，则∠2的度数是（　　）

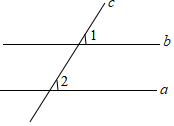A、120° B、60° C、45° D、30°

查看试题解析
2. 如图，直线AB∥CD ，则下列结论正确的是（）

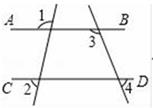A、∠1＝∠2 B、∠3＝∠4 C、∠1+∠3＝180° D、∠3+∠4＝180°

查看试题解析
3. 下列运算正确的是（　　）

A、x²+x³＝x⁵ B、（﹣2a²）³＝﹣8a⁶ C、x²•x³＝x⁶ D、x⁶÷x²＝x³

查看试题解析
4. 二元一次方程组 ${\begin{cases} 2 x + y = 5 k \\ 2 x - y = 7 k \end{cases}$ 的解满足方程 $\frac{1}{3}$ x﹣2y=5，那么k的值为（）

A、 $\frac{3}{5}$ B、 $\frac{5}{3}$ C、﹣5 D、1

查看试题解析
5. 如图，用直尺和三角尺画图：已知点P和直线a，经过点P作直线b，使b∥a，其画法的依据是（）

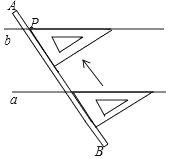A、同位角相等，两直线平行 B、两直线平行，同位角相等 C、过直线外一点有且只有一条直线与已知直线平行 D、内错角相等，两直线平行

查看试题解析
6. 方程3x+y=7的正整数解的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 要使多项式（x+p）（x﹣q）不含x的一次项，则p与q的关系是（　　）

A、相等 B、互为相反数 C、互为倒数 D、乘积为﹣1

查看试题解析
8. 已知2^a＝3，8^b＝6，2^2a^﹣3b+1的值为（　　）

A、3 B、 $\frac{3}{2}$ C、2 D、5

查看试题解析
9. 如图，在长为15，宽为12的矩形中，有形状、大小完全相同的5个小矩形，则图中阴影部分的面积为（）

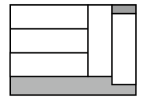A、35 B、45 C、55 D、65

查看试题解析
10. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE＝α，∠DCE＝β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，④360°﹣α﹣β，∠AEC的度数可能是（　　）

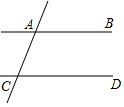A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题（本题有6个小题，每空3分，共21分）

11. 已知方程2x+3y﹣1＝0，用含x的代数式表示y，则．

查看试题解析
12. 某种病毒变异后的直径约为0.000 000 56米，将这个数用科学记数法表示为米.

查看试题解析
13. 小亮解方程组 ${\begin{cases} 2 x + y = ● \\ 2 x - y = 12 \end{cases}$ 的解为 ${\begin{cases} x = 5 \\ y = ★ \end{cases}$ ，由于不小心，滴上了两滴墨水，刚好遮住了两个数●和★，请你帮他找回★，这个数★＝， ●＝．

查看试题解析
14. 如图，将△ABC沿BC方向平移到△DEF，若A、D间的距离为1，CE＝2，则BF＝．

查看试题解析
15. 如图，将一条对边互相平行的纸带进行折叠，折痕为MN，若∠AMD′＝42°时，则∠MNC′＝度．

查看试题解析
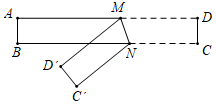16. 利用平方差计算（2+1）（2²+1）（2⁴+1）（2⁸+1）+1＝．

查看试题解析

三、解答题（本题有7小题，共49分）

17. 计算：

(1)、﹣l¹⁰⁰+ ${}^{3}{\sqrt{64}}$ ﹣ ${(\frac{1}{3})}^{- 1}$ +（π﹣2020）⁰；

(2)、 ${(\frac{1}{3} x y)}^{2} \cdot (- 12 x^{2} y^{2})$ ÷ $(- \frac{4}{3} x^{3} y)$ ．

查看试题解析
18. 计算：

(1)、（12a³﹣6a²+3a）÷3a﹣（2a﹣1）²

(2)、（x﹣6）（x+4）+（3x+2）（2﹣3x）

查看试题解析
19. 解方程组：

(1)、 ${\begin{cases} x + 2 y = 9 \\ 3 x - 2 y = - 1 \end{cases}$

(2)、 ${\begin{cases} \frac{x}{4} + \frac{y}{3} = 3 \\ 3 x - 2 (y - 1) = 11 \end{cases}$ ．

查看试题解析
20. 已知：如图，在△ABC中，点D、E分别在BC、AC上，且AB∥DE，∠1＝∠2．
求证：AF∥BC．

查看试题解析
21. 如图是用一些小长方形和小正方形拼成的一个大正方形．

(1)、在图①中根据图形面积的关系写出一个用乘法公式计算的等式；

(2)、如果a﹣b＝3，a²+b²＝15，试求图②中阴影部分的面积．

查看试题解析
22. 已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨．某物流公司现有34吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．
根据以上信息，解答下列问题：

(1)、1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？

(2)、请你帮该物流公司设计租车方案；

(3)、若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费．

查看试题解析