浙江省绍兴市越城区绍初教育集团2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-05-15 类型：期中考试

进入出卷网下载

一、选择题（每题3分）

1. 函数y＝ $\frac{1}{\sqrt{x + 2}}$ 的自变量x的取值范围是（　　）

A、x＞0 B、x≥﹣2 C、x＞﹣2 D、x≠﹣2

查看试题解析
2. 下列各式与 $\sqrt{3}$ 是同类二次根式的是（　　）

A、 $\sqrt{8}$ B、 $\sqrt{24}$ C、 $\sqrt{125}$ D、 $\sqrt{12}$

查看试题解析
3. 下列运算正确的是（　　）

A、 $\sqrt{5}$ ﹣ $\sqrt{3}$ ＝ $\sqrt{2}$ B、 $\sqrt{4 \frac{1}{9}}$ ＝2 $\frac{1}{3}$ C、4 $\sqrt{3}$ ×2 $\sqrt{6}$ ＝24 $\sqrt{2}$ D、 $\sqrt{6 - {(\sqrt{5})}^{2}}$ ＝6﹣ $\sqrt{5}$

查看试题解析
4. 有一组数据如下：3，a，4，6，7，它们的平均数是5，那么这组数据的方差是（　　）

A、10 B、 $\sqrt{10}$ C、2 D、 $\sqrt{2}$

查看试题解析
5. 如果关于x的一元二次方程k²x²﹣（2k+1）x+1＝0有两个实数根，那么k的取值范围是（　　）

A、k＞﹣ $\frac{1}{4}$ B、k＞﹣ $\frac{1}{4}$ 且k≠0 C、k＜﹣ $\frac{1}{4}$ D、k $\geq \frac{1}{4}$ 且k≠0

查看试题解析
6. 如果关于x的一元二次方程（m+1）x²+x+m²﹣2m﹣3＝0有一个根为0，则m的值（　　）

A、﹣1 B、3 C、﹣1或3 D、以上答案都不对

查看试题解析
7. 若α，β是方程x²﹣2x﹣3＝0的两个实数根，则α²+β²+αβ的值为（　　）

A、10 B、9 C、7 D、5

查看试题解析
8. 已知a，b，c分别是三角形的三边，则方程（a+b）x²+2cx+（a+b）＝0的根的情况是（　　）

A、没有实数根 B、可能有且只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析

二、填空题（每小题4分）

9. 某商品经过连续两次降价，销售单价由原来的125元降到80元，则平均每次降价的百分率为．

查看试题解析
10. 某中学随机调查了15名学生，了解他们一周在学校参加体育锻炼时间，列表如下：
锻炼时间（小时）
5
6
7
8
人数
2
6
5
2
则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是；．

查看试题解析
11. 如图所示的数轴上，点B与点C关于点A对称，A、B两点对应的实数是 $\sqrt{3}$ 和﹣1，则点C所对应的实数是．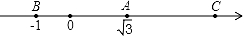

查看试题解析
12. 已知x为实数，且满足（2x²+3）²+2（2x²+3）﹣15＝0，则2x²+3的值为．

查看试题解析
13. 若1≤x≤5，化简 $\sqrt{{(x - 1)}^{2}}$ +|x﹣5|= ．

查看试题解析
14. 在等腰△ABC中，三边分别为a、b、c，其中a＝4，b、c恰好是方程x²﹣（2k+1）x+5（k﹣ $\frac{3}{4}$ ）＝0的两个实数根，则△ABC的周长为．

查看试题解析

三、解答题

15. 计算

(1)、2 $\sqrt{20}$ ﹣ $\sqrt{5}$ +2 $\sqrt{\frac{1}{5}}$ ；

(2)、 ${(\sqrt{2} + \sqrt{3})}^{2}$ ﹣ $(\sqrt{2} + \sqrt{3})$ $(\sqrt{2} - \sqrt{3})$ ；

(3)、已知：x＝1﹣ $\sqrt{2}$ ，y＝1+ $\sqrt{2}$ ，求x²+y²﹣xy的值．

查看试题解析
16. 选择适当的方法解下列方程：

(1)、（2x﹣1）²﹣4＝0；

(2)、 $\frac{3}{2} x^{2}$ ﹣x﹣2＝0．

查看试题解析
17. 为了解学生的课外阅读情况，李老师随机调查了一部分学生，得到了他们上周双休日课外阅读时间（记为t，单位：h）的一组样本数据，其部分条形图和扇形图如下：

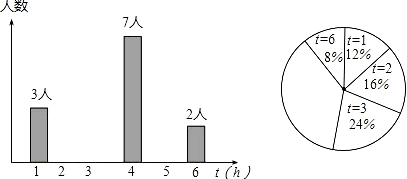(1)、请补全条形图和扇形图；

(2)、试确定这组样本数据的中位数和众数；

(3)、估计全班学生上周双休日的平均课外阅读时间．

查看试题解析
18. 一艘轮船以20海里/时的速度由西向东航行，在途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，距台风中心20海里的圆形区域（包括边界）都属于台风区域，当轮船到A处时测得台风中心移到位于点A正南方的B处，且AB＝100海里．若这艘轮船自A处按原速度继续航行，在途中是否会遇到台风？若会，则求出轮船最初遇到台风的时间；若不会，请说明理由．

查看试题解析
19. 商场某种商品平均每天可销售40件，每件盈利60元．为减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价1元，商场平均每天可多销售2件．

(1)、每件商品降价多少元时，商场日盈利可达到3150元？

(2)、商场日盈利能否达到3300元？

(3)、每件商品降价多少元时，商场日盈利最多？

查看试题解析
20. 如图，在△ABC中，AB＝AC＝13厘米，BC＝10厘米，AD⊥BC于点D，动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动．设动点运动时间为t秒．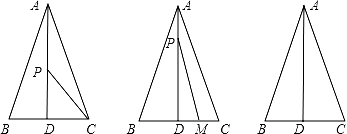

(1)、求AD的长；

(2)、当△PDC的面积为15平方厘米时，求t的值；

(3)、动点M从点C出发以每秒2厘米的速度在射线CB上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动．是否存在t，使得S_△PMD＝ $\frac{1}{12}$ S_△ABC？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析

锻炼时间（小时）	5	6	7	8
人数	2	6	5	2