江苏省盐城市盐都区2020届九年级下学期数学期中考试试卷
试卷更新日期：2020-05-15 类型：期中考试
一、单选题
-
1. 下列方程中，一元二次方程是（ ）A、x﹣1＝0 B、x2﹣3＝0 C、 D、x+y＝22. 下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A、正三角形 B、正五边形 C、正六边形 D、正七边形3. 下列一元二次方程中，没有实数根的是（ ）A、x2﹣2x＝0 B、x2﹣2x+1＝0 C、2x2﹣x﹣1＝0 D、2x2﹣x+1＝04. 如图是用相同正方形砖铺成的地面，一宝物藏在其中某一块砖的下面，则宝物在黑色区域的概率是（ ）
A、 B、 C、 D、5. 下列说法错误的是（ ）A、等弧所对的圆心角相等 B、弧的度数等于该弧所对的圆心角的度数 C、经过三点可以作一个圆 D、三角形的外心到三角形各顶点距离相等6. 北京奥运会的主会场“鸟巢”让人记忆深刻.在鸟巢设计的最后阶段，经过了两次优化，鸟巢的结构用钢量从5.4万吨减少到4.2万吨.若设平均每次用钢量降低的百分率为x，根据题意，可得方程（ ）A、5.4（1﹣x）2＝4.2 B、5.4（1﹣x2）＝4.2 C、5.4（1﹣2x）＝4.2 D、4.2（1+x）2＝5.47. 如图，点O是△ABC的内心，若∠A＝70°，则∠BOC的度数是（ ）
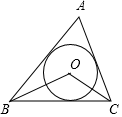A、120° B、125° C、130° D、135°8. 如图，在⊙O中，半径r＝10，弦AB＝16，P是弦AB上的动点（不含端点A，B），若线段OP长为正整数，则点P的个数有（ ）
A、4个 B、5个 C、6个 D、7个二、填空题
-
9. 方程x2﹣9=0的解是 ．10. 数据1，2，2，3，2，4的众数是.11. 设α、β是方程x2+x﹣3＝0的两个实数根，则α+β＝.12. 圆锥的底面半径为3，母线长为5，该圆锥的侧面积为.13. 甲、乙两名射击运动员各进行10次射击练习，总成绩均为95环，这两名运动员成绩的方差分别是S甲2=0.6，S乙2=0.4，则成绩更稳定的是 ．14. 如图，四边形ABCD是⊙O的内接四边形，∠B＝135°，则∠AOC的度数为.
15. 如图，在矩形ABCD中，AB=4，AD=2，以点A为圆心，AB长为半径画圆弧交边DC于点E，则 的长度为 ．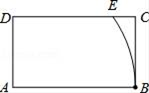
16. 如图，∠MON＝45°，一直角三角尺△ABC的两个顶点C、A分别在OM，ON上移动，若AC＝6，则点O到AC距离的最大值为.
三、解答题
-
17. 解下列方程：(1)、x2﹣4x﹣5＝0；(2)、（x+1）2＝2（x+1）.18. 有3个完全相同的小球，把它们分别标号为1，2，3，放在一个口袋中，随机地摸出一个小球不放回，再随机地摸出一个小球.(1)、采用树状图法（或列表法）列出两次摸球出现的所有可能结果；(2)、求摸出的两个球号码之和为偶数的概率.19. 已知关于x的一元二次方程x2﹣6x+c＝0(1)、若此方程有两个相等实数根，求此时c的值及方程的根；(2)、若此方程有一个根为5，求此时c的值及方程的另一根.20. 甲乙两位同学参加数学综合素质测试，各项成绩如下表：（单位：分）
数与代数
空间与图形
统计与概率
综合与实践
学生甲
93
93
89
90
学生乙
94
92
94
86
(1)、分别计算甲、乙同学成绩的中位数；(2)、如果数与代数，空间与图形，统计与概率，综合与实践的成绩按4：3：1：2计算，那么甲、乙同学的数学综合素质成绩分别为多少分？21. 如图，在Rt△ABC中，∠ACB＝90°.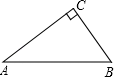
(1)、以AB边上一点O为圆心作⊙O，使⊙O经过点A，C；（保留作图痕迹，不写作法）(2)、判断点B与⊙O的位置关系是.（直接写出答案）22. 如图，AB是⊙O直径，CD为⊙O的切线，C为切点，过A作CD的垂线，垂足为D．
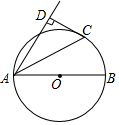(1)、求证：AC平分∠BAD；(2)、若⊙O半径为5，CD＝4，求AD的长．23. 阅读第（1）题的解题过程，再解答第（2）题：（ 1 ）例：解方程x2﹣|x|﹣2＝0.
解：当x≥0时，原方程可化为x2﹣x﹣2＝0.
解得：x1＝2，x2＝﹣1（不合题意.舍去）
当x＜0时，原方程可化为x2+x﹣2＝0.
解得：x1＝﹣2，x2＝1（不合题意.舍去）
∴原方程的解是x1＝2，x1＝﹣2.
（ 2 ）请参照上例例题的解法，解方程x2﹣x|x﹣1|﹣1＝0.
24. 如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC＝∠D＝60°.
(1)、求∠ABC的度数；(2)、求证：AE是⊙O的切线；(3)、当BC＝4时，求阴影部分的面积.25. 某旅行社的一则广告如下：
甲公司想分批组织员工到延安红色旅游学习.
(1)、如果第一批组织40人去学习，则公司应向旅行社交费元；(2)、如果公司计划用29250元组织第一批员工去学习，问这次旅游学习应安排多少人参加？26. 如图1，在Rt△ABC中，∠B＝90°，AB＝BC＝12cm，点D从点A出发沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC（点E、F分别在AC、BC上）.设点D移动的时间为t秒.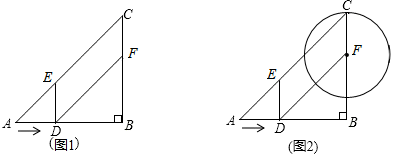
(1)、试判断四边形DFCE的形状，并说明理由；(2)、当t为何值时，四边形DFCE的面积等于20cm2？(3)、如图2，以点F为圆心，FC的长为半径作⊙F，在运动过程中，当⊙F与四边形DFCE只有1个公共点时，请直接写出t的取值范围.27. 某数学活动小组在一次活动中，对一个数学问题作如下探究：
(1)、（问题发现）如图1，AD，BD为⊙O的两条弦（AD＜BD），点C为 的中点，过C作CE⊥BD，垂足为E.求证：BE＝DE+AD.（问题探究）小明同学的思路是：如图2，在BE上截取BF＝AD，连接CA，CB，CD，CF.……请你按照小明的思路完成上述问题的证明过程.
(2)、（结论运用）如图3，△ABC是⊙O的内接等边三角形，点D是 上一点，∠ACD＝45°，连接BD，CD，过点A作AE⊥CD，垂足为E.若AB＝ ，则△BCD的周长为.(3)、（变式探究）如图4，若将（问题发现）中“点C为 的中点”改为“点C为优弧 的中点”，其他条件不变，上述结论“BE＝DE+AD”还成立吗？若成立，请说明理由；若不成立，请写出BE、AD、DE之间的新等量关系，并加以证明.