江苏省江阴市长泾片2020届九年级下学期数学期中考试试卷
试卷更新日期:2020-05-15 类型:期中考试
一、单选题
-
1. -3的倒数是( )A、 B、3 C、0 D、2. 函数y= 中自变量x的取值范围是( )A、x≠2 B、x≥2 C、x≤2 D、x>23. 下列因式分解正确的是( )A、 B、 C、 D、4. 某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述不正确的是( )A、众数是108 B、中位数是105 C、平均数是101 D、方差是935.
下列四个立体图形中,左视图为矩形的是( )
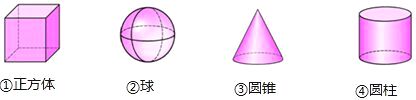 A、①③ B、①④ C、②③ D、③④6. 下列四个图案中,不是中心对称图案的是( )A、
A、①③ B、①④ C、②③ D、③④6. 下列四个图案中,不是中心对称图案的是( )A、 B、
B、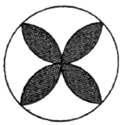 C、
C、 D、
D、 7. 菱形不具备的性质是( )A、四条边都相等 B、对角线一定相等 C、是轴对称图形 D、是中心对称图形8. 如图,弦AB的长等于⊙O的半径,点C在弧AMB上,则∠C的度数是( )
7. 菱形不具备的性质是( )A、四条边都相等 B、对角线一定相等 C、是轴对称图形 D、是中心对称图形8. 如图,弦AB的长等于⊙O的半径,点C在弧AMB上,则∠C的度数是( )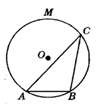 A、30º B、35º C、25º D、60º9. 如图,点A是反比例函数y= (x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为8,则k的值为( )
A、30º B、35º C、25º D、60º9. 如图,点A是反比例函数y= (x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为8,则k的值为( ) A、8 B、﹣8 C、4 D、﹣410. 如图,四边形 的顶点坐标分别为 ,当过点 的直线 将四边形 分成面积相等的两部分时,直线 所表示的函数表达式为( )
A、8 B、﹣8 C、4 D、﹣410. 如图,四边形 的顶点坐标分别为 ,当过点 的直线 将四边形 分成面积相等的两部分时,直线 所表示的函数表达式为( )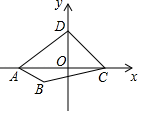 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的算术平方根是 .12. 据统计,全球每分钟约有850000000千克污水排入江河湖海,则850000000用科学记数法表示为.13. 计算:(3a+b)(3a﹣b)= .14. 某个函数具有性质:当x<0时,y随x的增大而减小,这个函数的表达式可以是(只要写出一个符合题意的答案即可).15. 若圆锥的底面周长为 ,母线长为6,则圆锥的侧面积等于.(结果保留π)16. 若函数y=kx﹣b的图象如图所示,则关于x的不等式k(x﹣3)﹣b>0的解集是.
 17. 如图,在△ABC中,AB=3,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则 的最大值为.
17. 如图,在△ABC中,AB=3,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则 的最大值为. 18. 如图,在矩形ABCD中,AB=3,BC=6,点E,F分别在BC,CD上,若BE= ,∠EAF=45°,则AF=.
18. 如图,在矩形ABCD中,AB=3,BC=6,点E,F分别在BC,CD上,若BE= ,∠EAF=45°,则AF=.
三、解答题
-
19. 计算:(1)、(2)、20.(1)、解方程:(2)、解不等式组:21. 如图,AB=AC,AD=AE,∠BAC=∠DAE.
 (1)、求证:△ABD≌△ACE;(2)、若∠1=25°,∠2=30°,求∠3的度数.22. 如图,在3 3的正方形网格中,点A、B、C、D、E、F都是格点.
(1)、求证:△ABD≌△ACE;(2)、若∠1=25°,∠2=30°,求∠3的度数.22. 如图,在3 3的正方形网格中,点A、B、C、D、E、F都是格点. (1)、从A、D、E、F四点中任意取一点,以所取点及B、C为顶点画三角形,那么所画三角形是等腰三角形的概率是.(2)、从A、D、E、F四点中任意取两点,以所取两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率.(请用“画树状图”或“列表”等方式写出分析过程)23. 某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
(1)、从A、D、E、F四点中任意取一点,以所取点及B、C为顶点画三角形,那么所画三角形是等腰三角形的概率是.(2)、从A、D、E、F四点中任意取两点,以所取两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率.(请用“画树状图”或“列表”等方式写出分析过程)23. 某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:a.七年级成绩频数分布直方图:
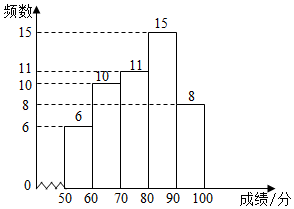
b.七年级成绩在 这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级
平均数
中位数
七
76.9
m
八
79.2
79.5
根据以上信息,回答下列问题:
(1)、在这次测试中,七年级在80分以上(含80分)的有人;(2)、表中m的值为;(3)、在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)、该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.24. 如图,在⊙O中,C,D分别为半径OB,弦AB的中点,连接CD并延长,交过点A的切线于点E. (1)、求证:AE⊥CE.(2)、若AE=2,sin∠ADE= ,求⊙O半径的长.25. 按要求作图,不要求写做法,但要保留作图痕迹.
(1)、求证:AE⊥CE.(2)、若AE=2,sin∠ADE= ,求⊙O半径的长.25. 按要求作图,不要求写做法,但要保留作图痕迹. (1)、如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.(2)、如图2,点E是菱形ABCD的对角线BD上一点,请只用直尺(不带刻度)作菱形AECF.26. 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)、如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.(2)、如图2,点E是菱形ABCD的对角线BD上一点,请只用直尺(不带刻度)作菱形AECF.26. 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形. (1)、已知 是比例三角形, , ,请直接写出所有满足条件的AC的长;(2)、如图1,在四边形ABCD中, ,对角线BD平分 , 求证: 是比例三角形.(3)、如图2,在 的条件下,当 时,求 的值.27. 在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A、B两点(点A在原点左侧),与y轴交于点C,且OB=2OA,连接AC、BC.
(1)、已知 是比例三角形, , ,请直接写出所有满足条件的AC的长;(2)、如图1,在四边形ABCD中, ,对角线BD平分 , 求证: 是比例三角形.(3)、如图2,在 的条件下,当 时,求 的值.27. 在平面直角坐标系xOy中,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A、B两点(点A在原点左侧),与y轴交于点C,且OB=2OA,连接AC、BC. (1)、求A、B两点的坐标;(2)、将线段AC绕点A旋转60°得到线段AC',若点C'在抛物线的对称轴上,求出此时抛物线的函数解析式.28. 如图,在Rt△ABC中,∠ACB=90°,AC、BC的长为方程x2﹣14x+a=0的两根,且AC﹣BC=2,D为AB的中点.
(1)、求A、B两点的坐标;(2)、将线段AC绕点A旋转60°得到线段AC',若点C'在抛物线的对称轴上,求出此时抛物线的函数解析式.28. 如图,在Rt△ABC中,∠ACB=90°,AC、BC的长为方程x2﹣14x+a=0的两根,且AC﹣BC=2,D为AB的中点.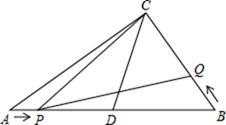 (1)、求a的值.(2)、动点P从点A出发,以每秒2个单位的速度,沿A→D→C的路线向点C运动;动点Q从点B出发,以每秒3个单位的速度,沿B→C的路线向点C运动,且点Q每运动1秒,就停止2秒,然后再运动1秒…若点P、Q同时出发,当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.
(1)、求a的值.(2)、动点P从点A出发,以每秒2个单位的速度,沿A→D→C的路线向点C运动;动点Q从点B出发,以每秒3个单位的速度,沿B→C的路线向点C运动,且点Q每运动1秒,就停止2秒,然后再运动1秒…若点P、Q同时出发,当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.①在整个运动过程中,设△PCQ的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围;
②是否存在这样的t,使得△PCQ为直角三角形?若存在,请直接写出所有符合条件的t的值.