江苏省江阴市青阳片2020年九年级下学期数学期中考试试卷
试卷更新日期：2020-05-15 类型：期中考试
一、单选题
-
1. －5的绝对值是（ ）A、±5 B、5 C、－5 D、2. 若分式 有意义，则x的取值范围是（ ）A、x ＞3 B、x ＜3 C、x =3 D、x ≠33. 下列运算中，正确的是 （ ）A、x2+5x2=6x4 B、x3 C、 D、4. 下列各项中，不是由平移设计的是（ ）A、
B、 
C、
D、
5. 下列六个数：0、 中，无理数出现的频数是（ ）A、3 B、4 C、5 D、66. 如果点P（-2，b）和点Q（a，-3）关于x轴对称，则 的值是（ ）A、1 B、-1 C、5 D、-57. 下列函数：①y=-x；②y=2x；③ ；④y=x2.当x<0时，y随x的增大而减小的函数有（ ）A、1个 B、2个 C、3个 D、4个8. 下表是某校合唱团成员的年龄分布，对于不同的x，下列关于年龄的统计量不会发生改变的是（ ）年龄/岁
13
14
15
16
频数
5
15
x
10- x
A、平均数、中位数 B、众数、方差 C、平均数、方差 D、众数、中位数9. 如图，抛物线 与 轴交于 两点， 是以点 为圆心， 为半径的圆上的动点， 是线段 的中点，连接 ，则线段 的最小值是（ ）
A、 B、 C、 D、10. 如图是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，m），且与x铀的一个交点在点（3，0）和（4，0）之间，则下列结论：①abc＞0；②a﹣b+c＞0；③b2＝4a（c﹣m）；④一元二次方程ax2+bx+c＝m+1有两个不相等的实数根，其中正确结论的个数是（ ）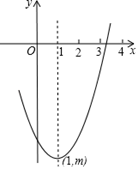
A、1 B、2 C、3 D、4二、填空题
-
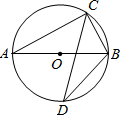
11. 我国第一艘航母“辽宁舰”最大排水量为67500吨，用科学记数法表示这个数字是吨．12. 因式分解：xy2﹣9x＝ ．13. “对顶角相等”的逆命题是命题（填真或假）14. 一次函数y=﹣2x+4的图象与x轴交点坐标是 ， 与y轴交点坐标是 ， 图象与坐标轴所围成的三角形面积是 ．15. 已知a、b满足方程组 ，则a+b的值为.16. 如图，AB为⊙O的直径，点C、D在⊙O上，若∠D＝20°，则∠CBA的度数是.
17. 设A（x1 ， y1），B（x2 ， y2）为函数 图象上的两点，且x1＜0＜x2 ， y1＞y2 ， 则实数k的取值范围是 ．18. 如图，在边长为1的菱形ABCD中，∠ABC＝60°，将△ABD沿射线BD的方向平移得到△A'B'D'，分别连接A'C，A'D，B'C，则A'C+B'C的最小值为.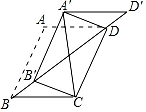
三、解答题
-
19.(1)、计算： －3tan60°＋ ；(2)、化简： .20.(1)、解方程：x2﹣2x﹣8=0；(2)、解不等式组21. 如图，在▱ABCD中，对角线AC，BD交于点O，经过点O的直线交AB于E，交CD于F.求证：OE＝OF.
22. 垃圾的分类处理与回收利用，可以减少污染，节省资源.某城市环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况，其相关信息如下：
根据图表解答下列问题：
(1)、请将条形统计图补充完整；(2)、在扇形统计图样中，产生的有害垃圾C所对应的圆心角度；(3)、调查发现，在可回收物中塑料类垃圾占13%，每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨，且全部分类处理，那么每月回收的塑料类垃圾可以获得多少吨二级原料？23. 甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.(1)、若从甲、乙两医院支援的医护人员中分别随机选1名，则所选的2名医护人员性别相同的概率是；
(2)、若从支援的4名医护人员中随机选2名，用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
24. 小明家的门框上装有一把防盗门锁（如图1），其平面结构图如图2所示，锁身可以看成由两条等弧 ， 和矩形ABCD组成的， 的圆心是倒锁按钮点M.已知 的弓形高GH=2cm，AD=8cm，EP=11cm.当锁柄PN绕着点N顺时针旋转至NQ位置时，门锁打开，此时直线PQ与 所在的圆相切，且PQ∥DN，tan∠NQP=2.
(1)、求 所在圆的半径；(2)、求线段AB的长度.（ ≈2.236，结果精确到0.1cm）25. 某种蔬菜每千克售价y1（元）与销售月份x之间的关系如图1所示，每千克成本y2（元）与销售月份x之间的关系如图2所示，其中图1中的点在同一条线段上，图2中的点在对称轴平行于y轴的同一条抛物线上，且抛物线的最低点的坐标为（6，1）.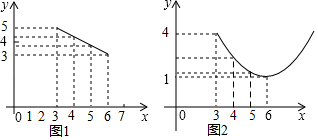
(1)、求出y1与x函数关系式；(2)、求出y2与x函数关系式；(3)、设这种蔬菜每千克收益为w元，试问在哪个月份出售这种蔬菜，w将取得最大值？并求出此最大值.（收益＝售价﹣成本）26. 实践与操作：我们在学习四边形的相关知识时，认识了平行四边形、矩形、菱形、正方形等一些特殊的四边形，下面我们用尺规作图的方法来体会它们之间的联系.如图，在▱ABCD中，AB＝4，BC＝6，∠ABC＝60°，请完成下列任务：
(1)、在图1中作一个菱形，使得点A、B为所作菱形的2个顶点，另外2个顶点在▱ABCD的边上；在图2中作一个菱形，使点B、D为所作菱形的2个顶点，另外2个顶点在▱ABCD的边上；（尺规作图，保留作图痕迹，不写作法）(2)、请在图形下方横线处写出你按（1）中要求作出的菱形的面积.27. 如图1，矩形ABCD的一边BC在直角坐标系中x轴上，折叠边AD，使点D落在x轴上点F处，折痕为AE，已知AB＝8，AD＝10，并设点B坐标为（m，0），其中m＜0.
(1)、求点E、F的坐标（用含m的式子表示）；(2)、连接OA，若△OAF是等腰三角形，求m的值；(3)、如图2，设抛物线y＝a（x﹣m+6）2+h经过A、E两点，其顶点为M，连接AM，若∠OAM＝90°，求a、h、m的值.28. 如图，在△ABC中，AB＝AC＝10cm，BD⊥AC于点D，BD＝8cm.点M从点A出发，沿AC的方向匀速运动，同时直线PQ由点B出发，沿BA的方向匀速运动，运动过程中始终保持PQ∥AC，直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM，设运动时间为t秒（0＜t≤5）.线段CM的长度记作y甲 ， 线段BP的长度记作y乙 ， y甲和y乙关于时间t的函数变化情况如图所示.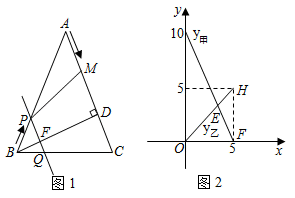
(1)、由图2可知，点M的运动速度是每秒cm；当t＝秒时，四边形PQCM是平行四边形？在图2中反映这一情况的点是（并写出此点的坐标）；(2)、设四边形PQCM的面积为ycm2 ， 求y与t之间的函数关系式；(3)、连接PC，是否存在某一时刻t，使点M在线段PC的垂直平分线上？若存在，求出此时t的值；若不存在，说明理由.