2015年辽宁省锦州市中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、单选题（本大题共8小题，每小题3分，共24分）

1. 2015的相反数是（　　）

A、2015 B、﹣2015 C、 $\frac{1}{2015}$ D、- $\frac{1}{2015}$

查看试题解析
2. 下列事件中，属于必然事件的是（　　）

A、明天我市下雨 B、抛一枚硬币，正面朝下 C、购买一张福利彩票中奖了 D、掷一枚骰子，向上一面的数字一定大于零

查看试题解析
3.
如图是由四个相同的小正方体组成的立体图形，它的左视图为（　　）

A、 B、 C、 D、

查看试题解析
4. 下列二次根式中属于最简二次根式的是（　　）

A、 $\sqrt{24}$ B、 $\sqrt{36}$ C、 $\sqrt{\frac{a}{b}}$ D、 $\sqrt{a + 4}$

查看试题解析
5. 在同一坐标系中，一次函数y=ax+2与二次函数y=x²+a的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
6. 如图，不等式组 $\{\begin{matrix} x + 2 > 0 \\ x - 2 \leq 0 \end{matrix}$ 的解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
7. 一元二次方程x²﹣2x+1=0的根的情况为（　　）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8.
如图，线段AB两个端点的坐标分别为A（4，4），B（6，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的 $\frac{1}{2}$ 后得到线段CD，则端点C和D的坐标分别为（　　）

A、（2，2），（3，2） B、（2，4），（3，1） C、（2，2），（3，1） D、（3，1），（2，2）

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分）

9. 已知地球上海洋面积约为316000000km² ， 316000000这个数用科学记数法可表示为 .

查看试题解析
10. 数据4，7，7，8，9的众数是 .

查看试题解析
11.
如图，已知l₁∥l₂ ， ∠A=40°，∠1=60°，∠2= .

查看试题解析
12. 分解因式：m²n﹣2mn+n= .

查看试题解析
13. 如表记录了一名球员在罚球线上投篮的结果．那么，这名球员投篮一次，投中的概率约为（精确到0.1）．
投篮次数（n）
50
100
150
200
250
300
500
投中次数（m）
28
60
78
104
123
152
251
投中频率（m/n）
0.56
0.60
0.52
0.52
0.49
0.51
0.50

查看试题解析
14.
如图，点A在双曲线y= $\frac{k}{x}$ 上，AB⊥x轴于点B，且△AOB的面积是2，则k的值是 .

查看试题解析
15. 制作某种机器零件，小明做220个零件与小芳做180个零件所用的时间相同，已知小明每小时比小芳多做20个零件．设小芳每小时做x个零件，则可列方程为 .

查看试题解析
16.
如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数 $y = \frac{1}{2} x$ 的图象上，从左向右第3个正方形中的一个顶点A的坐标为（6，2），阴影三角形部分的面积从左向右依次记为S₁、S₂、S₃、…、S_n ，则第4个正方形的边长是， S₃的值为．

查看试题解析

三、解答题（本大题共2小题，每小题8分，共16分）

17. 先化简，再求值：（1+ $\frac{1}{x - 1}$ ）÷ $\frac{x}{x^{2} - 1}$ ，其中：x= $3 \sqrt{2}$ ﹣3．

查看试题解析
18.
如图，在平面直角坐标系中，线段AB的两个端点是A（﹣5，1），B（﹣2，3），线段CD的两个端点是C（﹣5，﹣1），D（﹣2，﹣3）．
（1）线段AB与线段CD关于直线对称，则对称轴是　；
（2）平移线段AB得到线段A₁B₁ ，若点A的对应点A₁的坐标为（1，2），画出平移后的线段A₁B₁ ，并写出点B₁的坐标为　　．

查看试题解析

四、解答题

19.
2015年5月，某校组织了以“德润书香”为主题的电子小报制作比赛，评分结果只有60，70，80，90，100五种，现从中随机抽取部分作品，对其份数和成绩进行整理，制成如下两幅不完整的统计图：
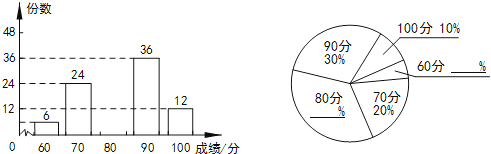
根据以上信息，解答下列问题：

(1)、求本次抽取了多少份作品，并补全两幅统计图；

(2)、已知该校收到参赛作品共900份，比赛成绩达到90分以上（含90分）的为优秀作品，据此估计该校参赛作品中，优秀作品有多少份？

查看试题解析
20. 育才中学计划召开“诚信在我心中”主题教育活动，需要选拔活动主持人，经过全校学生投票推荐，有2名男生和1名女生被推荐为候选主持人．

(1)、小明认为，如果从3名候选主持人中随机选拔1名主持人，不是男生就是女生，因此选出的主持人是男生和女生的可能性相同，你同意他的说法吗？为什么？

(2)、如果从3名候选主持人中随机选拔2名主持人，请通过列表或树状图求选拔出的2名主持人恰好是1名男生和1名女生的概率.

查看试题解析
21.
如图，△ABC中，点D，E分别是边BC，AC的中点，连接DE，AD，点F在BA的延长线上，且AF= $\frac{1}{2}$ AB，连接EF，判断四边形ADEF的形状，并加以证明．

查看试题解析
22.
如图，三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航，某一时刻航行到A处，测得该岛在北偏东30°方向，海监船以20海里/时的速度继续航行，2小时后到达B处，测得该岛在北偏东75°方向，求此时海监船与黄岩岛P的距离BP的长．（参考数据： $\sqrt{2}$ ≈1.414，结果精确到0.1）

查看试题解析
23.
如图，△ABC中，以AC为直径的⊙O与边AB交于点D，点E为⊙O上一点，连接CE并延长交AB于点F，连接ED．

(1)、若∠B+∠FED=90°，求证：BC是⊙O的切线；

(2)、若FC=6，DE=3，FD=2，求⊙O的直径．

查看试题解析
24.
开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价y（元/本）与购买数量x（本）之间的函数关系如图所示．

(1)、图中线段AB所表示的实际意义是　　；

(2)、请直接写出y与x之间的函数关系式；

(3)、已知该文具批发部这种笔记本的进价是3元/本，若小明购买此种笔记本超过10本但不超过20本，那么小明购买多少本时，该文具批发部在这次买卖中所获的利润W（元）最大？最大利润是多少？

查看试题解析
25.
如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．

(1)、如图①，当α=90°时，DE，DF，AD之间满足的数量关系是_____；

(2)、如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF= $\frac{1}{2}$ AD，请给出证明；

(3)、在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．

查看试题解析
26.
如图，在平面直角坐标系中，抛物线y=ax²+bx+2经过点A（﹣1，0）和点B（4，0），且与y轴交于点C，点D的坐标为（2，0），点P（m，n）是该抛物线上的一个动点，连接CA，CD，PD，PB．

(1)、求该抛物线的解析式；

(2)、当△PDB的面积等于△CAD的面积时，求点P的坐标；

(3)、当m＞0，n＞0时，过点P作直线PE⊥y轴于点E交直线BC于点F，过点F作FG⊥x轴于点G，连接EG，请直接写出随着点P的运动，线段EG的最小值．

查看试题解析

投篮次数（n）	50	100	150	200	250	300	500
投中次数（m）	28	60	78	104	123	152	251
投中频率（m/n）	0.56	0.60	0.52	0.52	0.49	0.51	0.50