浙江省宁波七中教育集团2019-2020学年九年级下学期数学第四次月考试卷
试卷更新日期:2020-05-14 类型:月考试卷
一、选择题(每小题4分,共48分)
-
1. -3的倒数等于( )A、9 B、-3 C、 D、2. 下列计算正确的是( )A、x+x=2x2 B、x-x=1 C、x·x=x2 D、x÷x= 03. 截止2020年4月12日,本次新冠病毒感染病例美国超55万人,其中55万用科学记数法表示为( )A、5.5x105 B、55×104 C、5.5×104 D、0.55×1064. 由5个大小相同的正方体组成的几何体如图所示,其主视图是( )
 A、
A、 B、
B、 C、
C、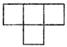 D、
D、 5. 一组数据1,1,1,3,5,7,现加入一个整数a,一定不会发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差6. 满足不等式组 整数解的和是( )A、2 B、3 C、4 D、57. 如图,∠AOB=100°,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( )
5. 一组数据1,1,1,3,5,7,现加入一个整数a,一定不会发生变化的统计量是( )A、平均数 B、中位数 C、众数 D、方差6. 满足不等式组 整数解的和是( )A、2 B、3 C、4 D、57. 如图,∠AOB=100°,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为( )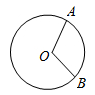 A、50° B、80°或50° C、130° D、50°或130°8. 如图,飞镖游戏板中每一块小正方形除颜色外都相同。若一个人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( )
A、50° B、80°或50° C、130° D、50°或130°8. 如图,飞镖游戏板中每一块小正方形除颜色外都相同。若一个人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是( )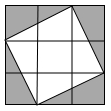 A、 B、 C、 D、9. “赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形。如果小正方形的面积为4, 大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于( )
A、 B、 C、 D、9. “赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形。如果小正方形的面积为4, 大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于( )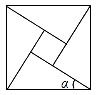 A、 B、 C、 D、10. 《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长。”则CD为( )
A、 B、 C、 D、10. 《九章算术》是我国古代著名数学著作,书中记载:“今有圆材,埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥DC于E,ED=1寸,AB=10寸,求直径CD的长。”则CD为( )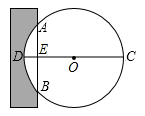 A、10寸 B、3寸 C、20寸 D、26寸11. 如图,∠A=∠B=∠C=∠D=∠E=∠F=60°,AB=3,BC=DE=1,CD=2,EF=0.5,则AG的长是( )
A、10寸 B、3寸 C、20寸 D、26寸11. 如图,∠A=∠B=∠C=∠D=∠E=∠F=60°,AB=3,BC=DE=1,CD=2,EF=0.5,则AG的长是( ) A、5.5 B、6 C、6.5 D、712. 一个大矩形按如图方式分割成16个小矩形,且只有标号为①②③的三个大小不同的小矩形为正方形,在满足条件的所有分割中,若知道16个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
A、5.5 B、6 C、6.5 D、712. 一个大矩形按如图方式分割成16个小矩形,且只有标号为①②③的三个大小不同的小矩形为正方形,在满足条件的所有分割中,若知道16个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )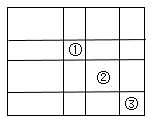 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题(每小题4分,共24分)
-
13. 在-2,2, 这三个实数中,最小的是。14. 因式分解:x2-x= .
15. 将抛物线y=x²先向上平移2个单位,再向左平移4个单位后的抛物线的解析式是。16. 有一个只含有x的代数式,x的值与代数式的值对应如下表:x
0
1
2
代数式的值
2
1
2
请写出两个符合上述条件的代数式,它可以是和。
17. 如图,在△ABC中,AB=AC, BC=12,E为AC的中点,线段BE的垂直平分线交边BC于D,设tan∠ACB=x,BD=y,则y与x的函数关系式是。 18. 如图,在Rt△AOB中,∠AOB=90°,AO=3,BO=4,将△AOB绕顶点O逆时针旋转α(0<α<90°),得到△A'OB',A'B'与OB相交于点E,若△OA'E为等腰三角形,则线段B'E的长度为。
18. 如图,在Rt△AOB中,∠AOB=90°,AO=3,BO=4,将△AOB绕顶点O逆时针旋转α(0<α<90°),得到△A'OB',A'B'与OB相交于点E,若△OA'E为等腰三角形,则线段B'E的长度为。
三、解答题(本大题有8小题,共78分)
-
19. 计算: -(π-2020)0+|2 -2|- 。20. 如图正方形网格中,每个小正方形的边长都为1。请在所给网格中按下列要求画出图形。
 (1)、在图1中以AB为边画一个等腰三角形ABC,使C在格点上,且另两边的长都是无理数;(2)、在图2中以AB为边画一个凸多边形,使多边形各顶点都在格点上且是中心对称图形,并且各边长都是无理数。21. 某学校环保小组为了解游客在某园区内购买瓶装饮料数量的情况,一天他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图1。
(1)、在图1中以AB为边画一个等腰三角形ABC,使C在格点上,且另两边的长都是无理数;(2)、在图2中以AB为边画一个凸多边形,使多边形各顶点都在格点上且是中心对称图形,并且各边长都是无理数。21. 某学校环保小组为了解游客在某园区内购买瓶装饮料数量的情况,一天他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图1。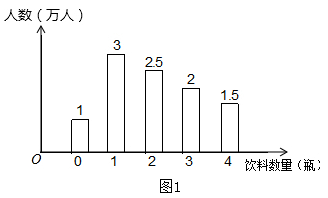
图2表一
出口
B
C
人均购买饮料数量(瓶)
3
2
(1)、在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的%。(2)、求A出口的被调查游客在园区内人均购买了多少瓶饮料?(3)、已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一(图2)所示,若C出口的被调查人数比B出口的被调查人数多2万,B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问B出口的被调查游客人数为多少万?22. 图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关。图2是其俯视简化示意图,已知轨道AB=120cm,两扇活页门的宽OC=OB=60cm,点B固定,当点C在AB上左右运动时,OC与OB的长度不变。 (1)、若∠OBC=53°,求AC的长。
(1)、若∠OBC=53°,求AC的长。(结果保留整数,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
(2)、当点C从点A向右运动60cm时,求点O在此过程中运动的路径长。23. 已知一次函数y=kx+2的图象与反比例函数y= 的图象交于点P,点P在第一象限。PA⊥x轴于点A,PB⊥y轴于点B。一次函数的图象分别交x轴、y轴于点C、D,且S△PBD=4, 。
(1)、求点D的坐标;(2)、求一次函数与反比例函数的解析式;(3)、直接写出当x>0时,一次函数的值大于反比例函数的值的x的取值范围。24. 空地上有一段长为20m的旧墙MN,小敏利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长100m。设AD=x(m),矩形菜园ABCD的面积为y(m²) . (1)、若x≤20,如图1,矩形菜园的一边靠墙,另三边一共用了100m木栏。
(1)、若x≤20,如图1,矩形菜园的一边靠墙,另三边一共用了100m木栏。①求y关于x的函数表达式,并写出自变量x的取值范围。
②当AD为多少米时,矩形菜园ABCD的面积最大,并求出最大值。
(2)、若x>20,如图2,且空地足够大,请你合理利用旧墙及所给木栏,帮小敏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求出最大值。25. 如果一个三角形的两个内角α,β满足α+2β=90°,那么我们称这样的三角形为“非常三角形”。 (1)、若△ABC是“非常三角形”,∠C>90°,∠A=50°,则∠B=。(2)、如图,△ABC中,AB=AC,D是边BC上一点,以BD为直径的⊙O经过点A,连结AD。
(1)、若△ABC是“非常三角形”,∠C>90°,∠A=50°,则∠B=。(2)、如图,△ABC中,AB=AC,D是边BC上一点,以BD为直径的⊙O经过点A,连结AD。①求证:△ADC为“非常三角形”。
②若sin B= ,AB=8,弦AB上是否存在一点P,使得△BDP是“非常三角形”,若存在,请求出线段AP的长度;若不存在,请说明理由。
26. 如图,在平面直角坐标系xOy中,抛物线y=ax²+bx+c与x轴交于点A(2,0)、B(6,0),与y轴交于点C(0,6),顶点为D,连结AC,作直线BC,点E是抛物线对称轴上的一个动点。 (1)、求出抛物线的解析式。(2)、若∠BCE=∠OCA,求点E的坐标。(3)、在(2)的条件下,延长CE交抛物线于点F,直接写出所有满足△GBD∽△FBC的点G的坐标。
(1)、求出抛物线的解析式。(2)、若∠BCE=∠OCA,求点E的坐标。(3)、在(2)的条件下,延长CE交抛物线于点F,直接写出所有满足△GBD∽△FBC的点G的坐标。