湖北省丹江口市2020届九年级下学期数学第一次月考试卷

试卷更新日期：2020-05-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 在数-1，0，2，-3中，绝对值最小的数是（）

A、 $- 1$ B、 $0$ C、 $2$ D、 $- 3$

查看试题解析
2. 如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°，则图中∠2的大小为（　　）

A、25° B、30° C、35° D、15°

查看试题解析
3. 下列左视图正确的是（　　）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $3 x \cdot 5 x = 8 x$ B、 ${(- 2 x)}^{3} = - 6 x^{3}$ C、 $\sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}$ D、 $2 \sqrt{x} - \sqrt{x} = \sqrt{x}$

查看试题解析
5. 在一次体育达标测试中，九年级（2）班15名男生的引体向上成绩如下表：问这15名男生的引体向上成绩的中位数和众数分别是（）

成绩/个

8

9

11

12

13

15

人数

1

2

3

4

3

2

A、12，13 B、12，12 C、11，12 D、3，4

查看试题解析
6. 如图，在△ABC中，AB=AC=6，点D在BC上，DE∥AC交AB于点E，DF∥AB交AC于点F则四边形DEAF的周长是（）

A、6 B、8 C、12 D、16

查看试题解析
7. 甲、乙两个搬运工搬运某种货物，已知乙比甲每小时多搬运600kg，甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等，求甲、乙两人每小时分别搬运多少千克货物.设甲每小时搬运xkg货物，则可列方程为（）

A、 $\frac{5000}{x - 600} = \frac{8000}{x}$ B、 $\frac{5000}{x} = \frac{8000}{x + 600}$ C、 $\frac{5000}{x + 600} = \frac{8000}{x}$ D、 $\frac{5000}{x} = \frac{8000}{x - 600}$

查看试题解析
8. 观察下面一列数：−1，2，−3，4，−5，6，−7…将这列数排成下列形式：记 $a_{i j}$ 为第i行第 $j$ 列的数，如 $a_{23}$ =4，那么 $a_{98}$ 是（）

A、56 B、72 C、88 D、98

查看试题解析
9. 如图所示，在扇形BAD中，点C在 $\vec{B D}$ 上，且∠BDC=30°，AB=2 $\sqrt{2}$ ，∠BAD=105°，过点C作CE⊥AD，则图中阴影部分的面积为（）

A、π﹣2 B、π﹣1 C、2π﹣2 D、2π+1

查看试题解析
10. 如图，矩形ABCD的顶点A在反比例函数y= $\frac{k}{x}$ （ $x > 0$ ）的图象上，顶点B、C在 $x$ 轴上，对角线DB的延长线交 $y$ 轴于点E，连接CE，若△BCE的面积是6，则 $k$ 的值为（）

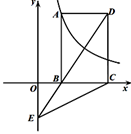A、6 B、12 C、9 D、18

查看试题解析

二、填空题

11. 分解因式：2a²﹣8= ．

查看试题解析
12. 某校九年级二班的学生在植树节开展“植树造林，绿化城市”的活动，本次活动结束后，该班植树情况的部分统计图如下所示，那么该班的总人数是人.

查看试题解析
13. 如图，四边形ABCD中，对角线AC、BD交于点O，且AC⊥BD，AC=BD，S_ABCD=8cm² ， E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长等于.

查看试题解析
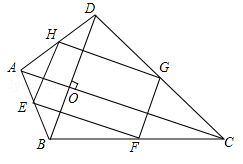14. 如图，△ABC是⊙O的内接三角形，连接OB、OC，若∠BAC+∠BOC=180°，BC=2 $\sqrt{3}$ cm，则⊙O的半径为cm.

查看试题解析
15. 规定：对于任意实数a，b都有：a⊕b=a（a-b）+1，其中等式右边是通常的加法、减法及乘法运算.如：2⊕5=2×（2-5）+1=2×（-3）+1=-5，那么等式3⊕x=16的解是.

查看试题解析
16.
如图，菱形ABCD的边长为2，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为．

查看试题解析

三、解答题

17. 计算： $3^{- 2} - {(π - 3)}^{0} + | \sqrt{3} - 2 |$

查看试题解析
18. 化简：（x+2+ $\frac{3 x + 4}{x - 2}$ ）÷ $\frac{x^{2} + 6 x + 9}{x - 2}$ .

查看试题解析
19. 如图，要测量小山上电视塔BC的高度，在山脚下点A测得：塔顶B的仰角为∠BAD=60°，塔底C的仰角为∠CAD=45°，AC=200米，求电视塔BC的高.

查看试题解析
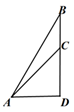20. 在一个不透明的口袋装有三个完全相同的小球，分别标号为1、2、3.求下列事件的概率：

(1)、从中任取一球，小球上的数字为偶数；

(2)、从中任取一球，记下数字作为点A的横坐标x，把小球放回袋中，再从中任取一球记下数字作为点A的纵坐标y，点A（x，y）在函数的图象上.

查看试题解析
21. 已知关于 $x$ 的方程 $x^{2} - (2 k + 1) x + k^{2} + 2 k = 0$ ，有两个实数根 $x_{1}$ ， $x_{2}$ .

(1)、求 $k$ 的取值范围；

(2)、若方程的两实数根 $x_{1}$ ， $x_{2}$ 满足 $x_{1} \cdot x_{2} - x_{1}^{2} - x_{2}^{2} = - 16$ ，求实数 $k$ 的值.

查看试题解析
22. 贫困户老王在精准扶贫工作队的帮扶下，在一片土地上种植了优质水果蓝莓，经核算，种植成本为18元/千克.今年正式上市销售，通过30天的试销发现：第1天卖出20千克；以后每天比前一天多卖4千克，销售价格 $y$ 元/千克）与时间x（天）之间满足如下表：

时间 $x$ （天）

（1≤x＜20）

（20≤x≤30）

销售价格y（元/千克）

-0.5x+38

25

（其中，x，y均为整数）

(1)、试销中销售量P（千克）与时间 $x$ （天）之间的函数关系式为.

(2)、求销售蓝莓第几天时，当天的利润w最大？最大利润是多少元？

(3)、求试销的30天中，当天利润w不低于870元的天数共有几天.

查看试题解析
23. 如图1，以△ABC的边AB为直径作⊙O，交AC于点E，BD平分∠ABE交AC于F，交圆O于点D，且∠BDE=∠CBE.

(1)、求证：BC是⊙O的切线；

(2)、如图2，延长ED交直线AB于点P，若PA=AO，DE=2，求 $\frac{P D}{D E}$ 的值及AO的长.

查看试题解析
24. 如图1，ABCD为正方形，将正方形的边CB绕点C顺时针旋转到CE，记∠BCE=α，连接BE，DE，过点C作CF⊥DE于F，交直线BE于H.

(1)、当α=60°时，如图1，则∠BHC=；

(2)、当45°＜α＜90°，如图2，线段BH、EH、CH之间存在一种特定的数量关系，请你通过探究，写出这个关系式：（不需证明）；

(3)、当90°＜α＜180°，其它条件不变（如图3），（2）中的关系式是否还成立？若成立，说明理由；若不成立，写出你认为成立的结论，并简要证明.

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x - 2$ 与x轴交于A、B两点，与y轴交于点C，已知A（–1，0），且直线BC的解析式为y= $\frac{1}{2}$ x-2，作垂直于x轴的直线 $x = m$ ，与抛物线交于点F，与线段BC交于点E（不与点B和点C重合）.

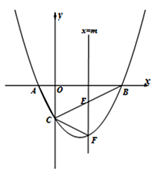(1)、求抛物线的解析式；

(2)、若△CEF是以CE为腰的等腰三角形，求m的值；

(3)、点P为y轴左侧抛物线上的一点，过点P作 $P M ⊥ B C$ 交直线BC于点M，连接PB，若以P、M、B为顶点的三角形与△ABC相似，求P点的坐标.

查看试题解析

时间 $x$ （天）	（1≤x＜20）	（20≤x≤30）
销售价格y（元/千克）	-0.5x+38	25

成绩/个	8	9	11	12	13	15
人数	1	2	3	4	3	2