河南省南阳市南召县2020届九年级网课摸底数学试卷
试卷更新日期:2020-05-14 类型:月考试卷
一、单选题
-
1. 如果抛物线 开口向下,那么 的取值范围为( )A、 B、 C、 D、2. 抛物线y=2x2+4与y轴的交点坐标是( )A、(0,2) B、(0,﹣2) C、(0,4) D、(0,﹣4)3. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
 A、AB=AD B、BC=CD C、 D、∠BCA=∠DCA4. 某课外兴趣小组为了解所在地区老年人的健康情况,分别作了四种不同的抽样调查,你认为抽样比较合理的是( )
A、AB=AD B、BC=CD C、 D、∠BCA=∠DCA4. 某课外兴趣小组为了解所在地区老年人的健康情况,分别作了四种不同的抽样调查,你认为抽样比较合理的是( )
A、调查了10名老年邻居的健康状况 B、在医院调查了1000名老年人的健康状况 C、在公园调查了1000名老年人的健康状况 D、利用派出所的户籍网随机调查了该地区10%的老年人的健康状况5. 对于二次函数 ,下列说法正确的是( )A、当 , 随 的增大而增大 B、当 时, 有最大值 C、图象的顶点坐标为 D、图象与 轴有一个交点6. 二次函数 变形为 的形式,正确的是( )A、 B、 C、 D、7. 如图, 的直径 与弦 的延长线交于点 ,若 , ,则 =( )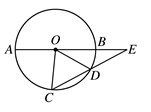 A、 B、 C、 D、8. 如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,⊙O的半径为 ,则弦CD的长为( )
A、 B、 C、 D、8. 如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,⊙O的半径为 ,则弦CD的长为( )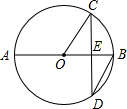 A、 B、3cm C、 D、9cm9. 一个圆的内接正六边形的边长为 2,则该圆的内接正方形的边长为( )A、 B、2 C、2 D、410. 如图,⊙O 是等边△ABC 的外接圆,其半径为 3,图中阴影部分的面积是( )
A、 B、3cm C、 D、9cm9. 一个圆的内接正六边形的边长为 2,则该圆的内接正方形的边长为( )A、 B、2 C、2 D、410. 如图,⊙O 是等边△ABC 的外接圆,其半径为 3,图中阴影部分的面积是( )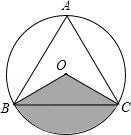 A、π B、 C、2π D、3π
A、π B、 C、2π D、3π二、填空题
-
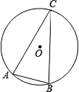
11. 函数 的顶点坐标是.12. 若点 , 是抛物线 上的两个点,则此抛物线的对称轴是.13. 如果点 与点 都在抛物线 上,那么 (填“>”、“<”或“=”)14. 如图, 是 的外接圆, , ,则 的半径为 .
 15. 如图,四边形 是平行四边形,经过点 , , 的 与 交于点 ,连接 ,若 ,则 °.
15. 如图,四边形 是平行四边形,经过点 , , 的 与 交于点 ,连接 ,若 ,则 °.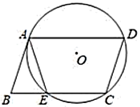
三、解答题
-
16. 先化简,再求值: ,在﹣2,0,1,2四个数中选一个合适的代入求值.17. 抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
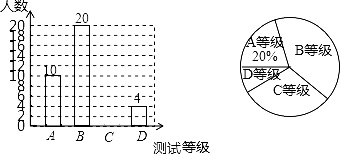 (1)、本次抽样调查共抽取了多少名学生?(2)、求测试结果为C等级的学生数,并补全条形图;(3)、若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?(4)、若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.18. 某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
(1)、本次抽样调查共抽取了多少名学生?(2)、求测试结果为C等级的学生数,并补全条形图;(3)、若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?(4)、若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.18. 某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)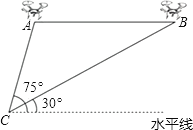 19. 如图,在 中, ,以 为直径的 交 于点 ,交 于点 , 是 的切线; 交 于点 .
19. 如图,在 中, ,以 为直径的 交 于点 ,交 于点 , 是 的切线; 交 于点 .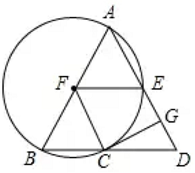 (1)、求证: ;(2)、填空:①若 的面积为 ,则 的面积为;
(1)、求证: ;(2)、填空:①若 的面积为 ,则 的面积为;②当 的度数为时,四边形 是菱形.
20. 某公司投入研发费用80万元(80万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为6元/件.此产品年销售量y(万件)与售价x(元/件)之间满足函数关系式y=﹣x+26.
(1)、求这种产品第一年的利润W1(万元)与售价x(元/件)满足的函数关系式;
(2)、该产品第一年的利润为20万元,那么该产品第一年的售价是多少?(3)、第二年,该公司将第一年的利润20万元(20万元只计入第二年成本)再次投入研发,使产品的生产成本降为5元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件.请计算该公司第二年的利润W2至少为多少万元.
21. 在平面直角坐标系中,直线 与x轴交于点B,与y轴交于点C,二次函数 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.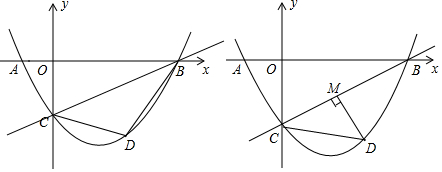 (1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.
(1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.