江苏省海安市八校2019-2020学年七年级下学期数学4月月考试卷

试卷更新日期：2020-05-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列说法错误的是（　　）

A、5是25的算术平方根 B、1是1的一个平方根 C、（-4）²的平方根是-4 D、0的平方根与算术平方根都是0

查看试题解析
2. 在实数 $\sqrt{5}$ 、 $\frac{22}{7}$ 、0、 $\sqrt[3]{- 1}$ 、3.1415、 $\sqrt{16}$ 、 $4. \overset{\cdot}{2} \overset{\cdot}{1}$ 、 $3 π$ 、6.1010010001…（相邻两个1之间的0依次增加1个）中，无理数的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 已知 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 是方程2x－ay＝3的一组解，那么a的值为（）

A、－5 B、－1 C、1 D、5

查看试题解析
4. 若m是任意实数，则点M(5 $+ m^{2}$ ，-1)在第（）象限.

A、一 B、二 C、三 D、四

查看试题解析
5. 已知点P(m，n)，且mn＞0，m+n＜0，则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 已知 $\sqrt[3]{1.51} = 1.147$ ， $\sqrt[3]{15.1} = 2.472$ ， $\sqrt[3]{0.151} = 0.5325$ ，则 $\sqrt[3]{1510}$ 的值是（）

A、24.72 B、53.25 C、11.47 D、114.7

查看试题解析
7. 如图，数轴上表示1， $\sqrt{3}$ 的点分别为A和B，若A为BC的中点，则点C表示的数是（）

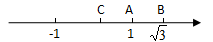A、 $\sqrt{3}$ －1 B、1－ $\sqrt{3}$ C、 $\sqrt{3}$ －2 D、2－ $\sqrt{3}$

查看试题解析
8. 如图所示，已知直线AB//ED，则∠B、∠C、∠D之间的关系为（）

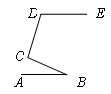A、∠B+∠C=∠D B、∠C+∠D-∠B=180° C、∠B+∠C+∠D=180° D、∠B+∠D-∠C=90°

查看试题解析
9. 为了丰富学生课外小组活动，培养学生动手操作能力，王老师让学生把5m长的彩绳截成2m或1m的彩绳，用来做手工编织，在不造成浪费的前提下，你有几种不同的截法（）

A、4 B、3 C、2 D、1

查看试题解析
10. 定义：直线a与直线b相交于点O，对于平面内任意一点M，点M到直线a与直线b的距离分别为p、q，则称有序实数对（p，q）是点M的“距离坐标”．根据上述定义，“距离坐标”是（1，2）的点的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 8的立方根是．

查看试题解析
12. 比较大小： $- \sqrt{3}$ $- \sqrt{5}$

查看试题解析
13. 若方程 $(a + 3) x^{| a | - 2} + 3 y = 1$ 是关于 $x ， y$ 的二元一次方程，则 $a$ =.

查看试题解析
14. 将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为.

查看试题解析
15. 已知点P（2a-6，a+1），若点P在坐标轴上，则点P的坐标为.

查看试题解析
16. 由方程组 ${\begin{matrix} 2 x + m = 1 \\ y - 3 = m \end{matrix}$ 可得出 $x$ 与 $y$ 关系是

查看试题解析
17. 已知1-3m是数A的一个平方根，4m-2是数A的算术平方根，则数A= .

查看试题解析
18. 如果∠A的两边分别与∠B的两边平行，且∠A比∠B的3倍少40°，则这两个角的度数分别为.

查看试题解析
19. 当k=时，关于x、y的二元一次方程组 ${\begin{matrix} 2 x + 3 y = k \\ 3 x + 2 y = k + 2 \end{matrix}$ 的解满足 $x + y = 2$ .

查看试题解析
20. 如图，在平面直角坐标系中，已如点A（1，1），B（-1，1），C（-1，-2），D（1，-2），把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处，并按 $A \to B \to C \to D \to A$ 的规律紧绕在四边形ABCD的边上，则细线的另一端所在位置的点的坐标是.

查看试题解析
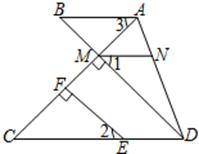
21. 完成下面的证明.
已知，如图所示，

BCE，AFE是直线，

AB∥CD，∠1=∠2，∠3=∠4.

求证：AD∥BE

证明：∵ AB∥CD （已知）

∴ ∠4 =∠▲（▲）

∵ ∠3 =∠4 （已知）

∴ ∠3 =∠▲ （▲）

∵∠1 =∠2 （已知）

∴∠1+∠CAF =∠2+ ∠CAF (▲)

即：∠▲=∠▲.

∴ ∠3 =∠▲（▲）

∴ AD∥BE（▲）

查看试题解析

三、解答题

22. 计算：

(1)、 $\sqrt{\frac{1}{4}} + \sqrt{{0.5}^{2}} - \sqrt[3]{8}$ ；

(2)、 $\sqrt[3]{- 8} + | \sqrt{3} - 2 | + \sqrt{{(- 3)}^{2}}$ .

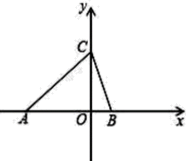
查看试题解析
23. 解下列方程组：

(1)、 ${\begin{array}{l} y - x = - 3 \\ 7 x - 5 y = 9 \end{array}$ （代入法）；

(2)、 ${\begin{matrix} 2 x + y = 5 \\ 3 x - 2 y = 11 \end{matrix}$ （加减法）；

(3)、 ${\begin{matrix} \frac{a}{3} = \frac{b}{4} = \frac{c}{5} \\ 2 a - 3 b + c = 6 \end{matrix}$ .

查看试题解析
24. 对于实数a，b，定义关于“ $\oplus$ ”的一种运算：a $\oplus$ b=2a+b，例如3 $\oplus$ 4=2×3+4=10.若x $\oplus$ （-y）=2，(2y) $\oplus$ x=1，求x+y的平方根.

查看试题解析
25. 如图，△ABC在直角坐标系中，

(1)、请写出△ABC各顶点的坐标；

(2)、若把△ABC向上平移2个单位，再向左平移1个单位得到△A′B′C′，写出A′、B′、C′的坐标，并在图中画出平移后图形；

(3)、求出△ABC的面积.

查看试题解析
26. 某高校共有5个大餐厅和2个小餐厅．经过测试：同时开放1个大餐厅、2个小餐厅，可供1680名学生就餐；同时开放2个大餐厅、1个小餐厅，可供2280名学生就餐．

(1)、求1个大餐厅、1个小餐厅分别可供多少名学生就餐；

(2)、若7个餐厅同时开放，能否供全校的5300名学生就餐？请说明理由．

查看试题解析
27. 已知，如图，EF⊥AC于F，DB⊥AC于M，∠1=∠2，∠3=∠C.

(1)、求证：AB//MN.

查看试题解析
28. 在平面直角坐标系中，已知点A（a，0），B (b，0)，a、b满足方程组 ${\begin{array}{l} a + b = - 2 \\ a - b = - 4 \end{array}$ ，C为y轴正半轴上一点，且 $S_{△ A B C} = 6$ .

(1)、求A、B、C三点的坐标；

(2)、是否存在点D（t，-t）使 $S_{Δ A B D} = \frac{1}{3} S_{Δ A B C}$ ？若存在，请求出D点坐标；若不存在，请说明理由.

(3)、已知E(-2，-4)，若坐标轴上存在一点P，使 $S_{△ P O E} = S_{△ A B C}$ ，请求出P的坐标.

查看试题解析