2015年辽宁省丹东市中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、单选题：下列各题的备选答案中，只有一个是正确的.每小题3分，共24分

1. ﹣2015的绝对值是（　　）

A、﹣2015 B、2015 C、 $\frac{1}{2015}$ D、 $- \frac{1}{2015}$

查看试题解析
2. 据统计，2015年在“情系桃源，好运丹东”的鸭绿江桃花观赏活动中，6天内参与人次达27.8万．用科学记数法将27.8万表示为（　　）

A、2.78×10⁶ B、27.8×10⁶ C、2.78×10⁵ D、27.8×10⁵

查看试题解析
3.
如图，是某几何体的俯视图，该几何体可能是（　　）

A、圆柱 B、圆锥 C、球 D、正方体

查看试题解析
4. 如果一组数据2，4，x，3，5的众数是4，那么该组数据的平均数是（　　）

A、5.2 B、4.6 C、4 D、3.6

查看试题解析
5. 下列计算正确的是（　　）

A、2a+a=3a² B、4^﹣²= $- \frac{1}{16}$ C、 $\sqrt{9}$ =±3 D、（a³）²=a⁶

查看试题解析
6.
如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（　　）

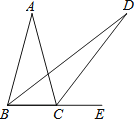A、15° B、17.5° C、20° D、22.5°

查看试题解析
7.
过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．若AB= $\sqrt{3}$ ， ∠DCF=30°，则EF的长为（　　）

A、2 B、3 C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
8. 一次函数y=﹣x+a﹣3（a为常数）与反比例函数 $y = - \frac{4}{x}$ 的图象交于A、B两点，当A、B两点关于原点对称时a的值是（　　）

A、0 B、-3 C、3 D、4

查看试题解析

二、填空题（每小题3分，共24分）

9.
如图，正六边形卡片被分成六个全等的正三角形．若向该六边形内投掷飞镖，则飞镖落在阴影区域的概率为 .

查看试题解析
10.
如图，∠1=∠2=40°，MN平分∠EMB，则∠3= .

查看试题解析
11. 分解因式：3x²﹣12x+12= .

查看试题解析
12. 若a＜ $\sqrt{6}$ ＜b，且a、b是两个连续的整数，则a^b= .

查看试题解析
13. 不等式组 $\{\begin{matrix} - 2 x + 3 < 5 \\ 3 x - 2 < 1 \end{matrix}$ 的解集为。

查看试题解析
14. 在菱形ABCD中，对角线AC，BD的长分别是6和8，则菱形的周长是 .

查看试题解析
15. 若x=1是一元二次方程x²+2x+a=0的一个根，那么a= .

查看试题解析
16.
如图，直线OD与x轴所夹的锐角为30°，OA₁的长为1，△A₁A₂B₁、△A₂A₃B₂、△A₃A₄B₃…△A_nA_n+1B_n均为等边三角形，点A₁、A₂、A₃…A_n+1在x轴的正半轴上依次排列，点B₁、B₂、B₃…B_n在直线OD上依次排列，那么点B_n的坐标为 .

查看试题解析

三、解答题

17. 先化简，再求值：（1﹣ $\frac{1}{a + 2}$ ）÷ $\frac{a^{2} - 1}{a + 2}$ ，其中a=3．

查看试题解析
18.
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．
（1）请画出△A₁B₁C₁ ，使△A₁B₁C₁与△ABC关于x轴对称；
（2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A₂B₂C₂ ，并直接写出点B旋转到点B₂所经过的路径长．

查看试题解析
19.
某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况，随机调查了部分学生最喜爱哪一类节目（被调查的学生只选一类并且没有不选择的），并将调查结果制成了如下的两个统计图（不完整）．请你根据图中所提供的信息，完成下列问题：

(1)、求本次调查的学生人数；

(2)、请将两个统计图补充完整，并求出新闻节目在扇形统计图中所占圆心角的度数；

(3)、若该中学有2000名学生，请估计该校喜爱电视剧节目的人数．

查看试题解析
20. 从甲市到乙市乘坐高速列车的路程为180千米，乘坐普通列车的路程为240千米．高速列车的平均速度是普通列车的平均速度的3倍．高速列车的乘车时间比普通列车的乘车时间缩短了2小时．高速列车的平均速度是每小时多少千米？

查看试题解析
21. 一个不透明的口袋中装有4个分别标有数字﹣1，﹣2，3，4的小球，它们的形状、大小完全相同．小红先从口袋中随机摸出一个小球记下数字为x；小颖在剩下的3个小球中随机摸出一个小球记下数字为y．

(1)、小红摸出标有数字3的小球的概率是___；

(2)、请用列表法或画树状图的方法表示出由x，y确定的点P（x，y）所有可能的结果；

(3)、若规定：点P（x，y）在第一象限或第三象限小红获胜；点P（x，y）在第二象限或第四象限则小颖获胜．请分别求出两人获胜的概率．

查看试题解析
22.
如图，AB是⊙O的直径，，连接ED、BD，延长AE交BD的延长线于点M，过点D作⊙O的切线交AB的延长线于点C．

(1)、若OA=CD= $2 \sqrt{2}$ ，求阴影部分的面积；

(2)、求证：DE=DM．

查看试题解析
23.
如图，线段AB，CD表示甲、乙两幢居民楼的高，两楼间的距离BD是60米．某人站在A处测得C点的俯角为37°，D点的俯角为48°（人的身高忽略不计），求乙楼的高度CD．（参考数据：sin37°≈ $\frac{3}{5}$ ， tan37°≈ $\frac{3}{4}$ ， sin48°≈ $\frac{7}{10}$ ， tan48°≈ $\frac{11}{10}$ ）

查看试题解析
24. 某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）与每件销售价x（元）的关系数据如下：
x
30
32
34
36
y
40
36
32
28

(1)、已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式（不写出自变量x的取值范围）；

(2)、如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？

(3)、设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？

查看试题解析
25.
在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN=90°．

(1)、如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；

(2)、将图1中的Rt△PMN绕点O顺时针旋转角度α（0°＜α＜45°）．
①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
②如图2，在旋转过程中，当∠DOM=15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP时，猜想此时PE与PF的数量关系，并给出证明；当BD=m•BP时，请直接写出PE与PF的数量关系．

查看试题解析
26.
如图，已知二次函数y=ax²+ $\frac{3}{2}$ x+c的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．

(1)、请直接写出二次函数y=ax²+ $\frac{3}{2}$ x+c的表达式；

(2)、判断△ABC的形状，并说明理由；

(3)、若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，请直接写出此时点N的坐标；

(4)、若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．

查看试题解析