2015年辽宁省本溪市中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、单选题：本大题共10小题，每小题3分，共30分

1. 实数﹣ $\frac{1}{2}$ 的相反数是（　　）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、2 D、-2

查看试题解析
2.
如图是由多个完全相同的小正方体组成的几何体，其左视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（　　）

A、 $5 m + 2 m = 7 m^{2}$ B、 $- 2 m^{2} \cdot m^{3} = 2 m^{5}$ C、 ${(- a^{2} b)}^{3} = - a^{6} b^{3}$ D、 $(b + 2 a) (2 a - b) = b^{2} - 4 a^{2}$

查看试题解析
4. 下列图案中既是轴对称图形，又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了A、B两类玩具，其中A类玩具的进价比B类玩具的进价每个多3元，经调查：用900元购进A类玩具的数量与用750元购进B类玩具的数量相同．设A类玩具的进价为m元/个，根据题意可列分式方程为（　　）

A、 $\frac{900}{m} = \frac{750}{m + 3}$ B、 $\frac{900}{m + 3} = \frac{750}{m}$ C、 $\frac{900}{m} = \frac{750}{m - 3}$ D、 $\frac{900}{m - 3} = \frac{750}{m}$

查看试题解析
6. 射击训练中，甲、乙、丙、丁四人每人射击10次，平均环数均为8.7环，方差分别为S_甲²=0.51，S_乙²=0.41、S_丙²=0.62、S_丁²=0.45，则四人中成绩最稳定的是（　　）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（　　）

A、16个 B、20个 C、25个 D、30个

查看试题解析
8.
如图，▱ABCD的周长为20cm，AE平分∠BAD，若CE=2cm，则AB的长度是（　　）

A、10cm B、8cm C、6cm D、4cm

查看试题解析
9.
如图，在平面直角坐标系中，直线AB与x轴交于点A（﹣2，0），与x轴夹角为30°，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线y= $\frac{k}{x}$ （k≠0）上，则k的值为（　　）

A、4 B、-2 C、 $\sqrt{3}$ D、- $\sqrt{3}$

查看试题解析
10.
如图，在△ABC中，∠C=90°，点P是斜边AB的中点，点M从点C向点A匀速运动，点N从点B向点C匀速运动，已知两点同时出发，同时到达终点，连接PM、PN、MN，在整个运动过程中，△PMN的面积S与运动时间t的函数关系图象大致是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题（本题共8小题，每小题3分，共24分）

11. 据《本溪日报》报道：本溪市高新区2015年1月份公共财政预算收入完成259 610 000元，首月实现税收收入“开门红”．将259 610 000用科学记数法表示为 .

查看试题解析
12. 分解因式：9a³﹣ab²= .

查看试题解析
13.
如图，直线a∥b，三角板的直角顶点A落在直线a上，两条直线分别交直线b于B、C两点．若∠1=42°，则∠2的度数是．

查看试题解析
14. 从﹣1、 $- \frac{1}{2}$ 、1这三个数中任取两个不同的数作为点A的坐标，则点A在第二象限的概率是．

查看试题解析
15. 关于x的一元二次方程（k﹣1）x²﹣2x+1=0有两个不相等的实数根，则实数k的取值范围是．

查看试题解析
16.
如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE= ．

查看试题解析
17. 在△ABC中，AB=6cm，AC=5cm，点D、E分别在AB、AC上．若△ADE与△ABC相似，且S_△_ADE：S_四边形_BCED=1：8，则AD= cm．

查看试题解析
18.
如图，已知矩形ABCD的边长分别为a，b，连接其对边中点，得到四个矩形，顺次连接矩形AEFG各边中点，得到菱形I₁；连接矩形FMCH对边中点，又得到四个矩形，顺次连接矩形FNPQ各边中点，得到菱形I₂；…如此操作下去，得到菱形I_n ，则I_n的面积是．

查看试题解析

三、解答题

19. 先化简，再求值：（x﹣2+ $\frac{3}{x + 2}$ ）÷ $\frac{x^{2} + 2 x + 1}{x + 2}$ ，其中x=（π﹣2015）⁰﹣ $\sqrt{4}$ +（ $\frac{1}{3}$ ）^﹣1 ．

查看试题解析
20.
某中学为开拓学生视野，开展“课外读书周”活动，活动后期随机调查了九年级部分学生一周的课外阅读时间，并将结果绘制成两幅不完整的统计图，请你根据统计图的信息回答下列问题：

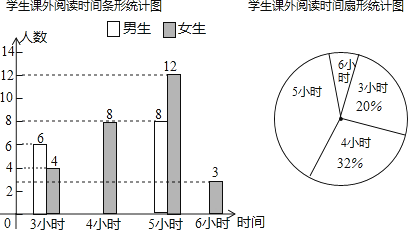(1)、本次调查的学生总数为____人，被调查学生的课外阅读时间的中位数是___小时，众数是___小时；

(2)、请你补全条形统计图；

(3)、在扇形统计图中，课外阅读时间为5小时的扇形的圆心角度数是；

(4)、若全校九年级共有学生700人，估计九年级一周课外阅读时间为6小时的学生有多少人？

查看试题解析
21. 暑期临近，本溪某旅行社准备组织“亲子一家游”活动，去我省沿海城市旅游，报名的人数共有69人，其中成人的人数比儿童人数的2倍少3人．

(1)、旅游团中成人和儿童各有多少人？

(2)、旅行社为了吸引游客，打算给游客准备一件T恤衫，成人T恤衫每购买10件赠送1件儿童T恤衫（不足10件不赠送），儿童T恤衫每件15元，旅行社购买服装的费用不超过1200元，请问每件成人T恤衫的价格最高是多少元？

查看试题解析
22.
张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据： $\sqrt{3}$ ≈1.732）

查看试题解析
23.
如图，点D是等边△ABC中BC边的延长线上一点，且AC=CD，以AB为直径作⊙O，分别交边AC、BC于点E、点F

(1)、求证：AD是⊙O的切线；

(2)、连接OC，交⊙O于点G，若AB=4，求线段CE、CG与 $\overset{\land}{C E}$ 围成的阴影部分的面积S．

查看试题解析
24. 某种商品的进价为40元/件，以获利不低于25%的价格销售时，商品的销售单价y（元/件）与销售数量x（件）（x是正整数）之间的关系如下表：
x（件）
…
5
10
15
20
…
y（元/件）
…
75
70
65
60
…

(1)、由题意知商品的最低销售单价是___元，当销售单价不低于最低销售单价时，y是x的一次函数．求出y与x的函数关系式及x的取值范围；

(2)、在（1）的条件下，当销售单价为多少元时，所获销售利润最大，最大利润是多少元？

查看试题解析
25.
如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）

(1)、
当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD__∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是_____；

(2)、
当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD= $\sqrt{3}$ AD；

(3)、将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．

查看试题解析
26.
如图，抛物线y=ax²+bx（a≠0）经过点A（2，0），点B（3，3），BC⊥x轴于点C，连接OB，等腰直角三角形DEF的斜边EF在x轴上，点E的坐标为（﹣4，0），点F与原点重合

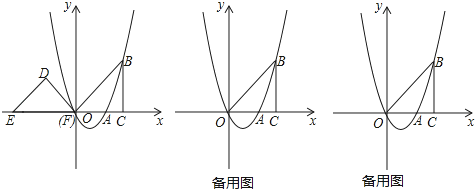(1)、求抛物线的解析式并直接写出它的对称轴；

(2)、△DEF以每秒1个单位长度的速度沿x轴正方向移动，运动时间为t秒，当点D落在BC边上时停止运动，设△DEF与△OBC的重叠部分的面积为S，求出S关于t的函数关系式；

(3)、点P是抛物线对称轴上一点，当△ABP是直角三角形时，请直接写出所有符合条件的点P坐标．

查看试题解析

x（件）	…	5	10	15	20	…
y（元/件）	…	75	70	65	60	…