浙江省温州2020年数学中考一模试卷
试卷更新日期:2020-05-12 类型:中考模拟
一、单选题
-
1. 下列各数中是负数的是( )A、 B、﹣3 C、 D、2. 下列方程中,是一元一次方程的为( )A、3x+2y=6 B、4x-2=x+1 C、x2+2x-1=0 D、 -3=3. 下列各项中,不是由平移设计的是( )A、
 B、
B、  C、
C、 D、
D、 4. 下列六个数:0、 、 、 、- 、 中,无理数出现的频数是( ).A、3 B、4 C、5 D、65. 下列运算正确的是( )A、a15÷b5=a3 B、4a•3a2=12a2 C、(a﹣b)2=a2﹣b2 D、(2a2)2=4a46. 如果点P(-2,b)和点Q(a,-3)关于x轴对称,则 的值是( )A、1 B、-1 C、5 D、-57. 如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB—BC的路径运动,到点C停止运动.过点E作EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是( )
4. 下列六个数:0、 、 、 、- 、 中,无理数出现的频数是( ).A、3 B、4 C、5 D、65. 下列运算正确的是( )A、a15÷b5=a3 B、4a•3a2=12a2 C、(a﹣b)2=a2﹣b2 D、(2a2)2=4a46. 如果点P(-2,b)和点Q(a,-3)关于x轴对称,则 的值是( )A、1 B、-1 C、5 D、-57. 如图,在正方形ABCD中,AB=4cm,动点E从点A出发,以1cm/秒的速度沿折线AB—BC的路径运动,到点C停止运动.过点E作EF∥BD,EF与边AD(或边CD)交于点F,EF的长度y(cm)与点E的运动时间x(秒)的函数图象大致是( )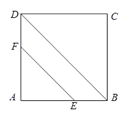 A、
A、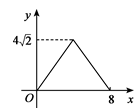 B、
B、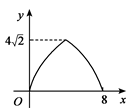 C、
C、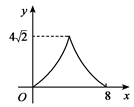 D、
D、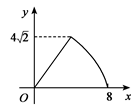 8. 如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y= (x>0)的图象上,则△OAB的面积等于( )
8. 如图,在平面直角坐标系中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y= (x>0)的图象上,则△OAB的面积等于( )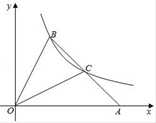 A、2 B、3 C、4 D、69. 某校九年级(1)班在举行元旦联欢会时,班长觉得快要毕业了,决定临时增加一个节目:班里面任意两名同学都要握手一次.小张同学统计了一下,全班同学共握手了465次.你知道九年级(1)班有多少名同学吗?设九年级(1)班有x名同学,根据题意列出的方程是( )
A、2 B、3 C、4 D、69. 某校九年级(1)班在举行元旦联欢会时,班长觉得快要毕业了,决定临时增加一个节目:班里面任意两名同学都要握手一次.小张同学统计了一下,全班同学共握手了465次.你知道九年级(1)班有多少名同学吗?设九年级(1)班有x名同学,根据题意列出的方程是( ) A、 =465 B、 =465 C、x(x﹣1)=465 D、x(x+1)=46510. 如图,△ABC中,AC=3,BC= ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A、 =465 B、 =465 C、x(x﹣1)=465 D、x(x+1)=46510. 如图,△ABC中,AC=3,BC= ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( ) A、 -1 B、7-4 C、 D、1
A、 -1 B、7-4 C、 D、1二、填空题
-
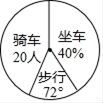
11. 因式分解:xy2﹣9x= .12. 已知a、b满足方程组 ,则a+b的值为.13. 如图是七年级(21)班学生上学的不同方式的扇形统计图,若步行人数所占的圆心角的度数为72°,坐车的人数占40%,骑车人数为20人,则该班人数为人.
 14. 两条相交直线 与 的图象如图所示,当 时, .
14. 两条相交直线 与 的图象如图所示,当 时, . 15. 如图,点A在双曲线y= 的第一象限的那一支上,AB垂直于x轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.
15. 如图,点A在双曲线y= 的第一象限的那一支上,AB垂直于x轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.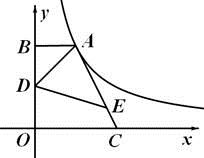 16. 如图,在菱形 中, 为边 的中点, 为边 上一动点(不与 重合),将 沿直线 折叠,使点 落在点 处,连接 , ,当 为等腰三角形时, 的长为.
16. 如图,在菱形 中, 为边 的中点, 为边 上一动点(不与 重合),将 沿直线 折叠,使点 落在点 处,连接 , ,当 为等腰三角形时, 的长为.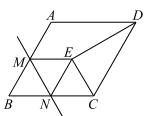
三、解答题
-
17.(1)、计算: ;(2)、解方程: +2= .18. 已知:如图,在平面直角坐标系中.
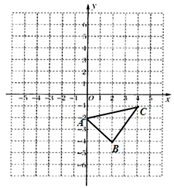
①作出△ABC关于 轴对称的 ,并写出 三个顶点的坐标;
②直接写出△ABC的面积为 ▲ ;
③在x轴上画点P,使PA+PC最小.
19. 已知:如图,在▱ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.求证:BF=DE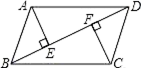 20. 每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
20. 每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
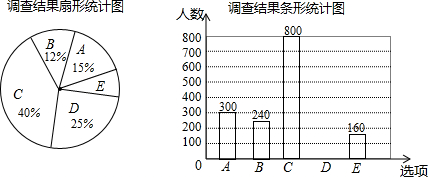
根据以上统计图,解答下列问题:
(1)、本次接受调查的市民共有人;(2)、扇形统计图中,扇形E的圆心角度数是;
(3)、请补全条形统计图;(4)、若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
21. 已知,如图,抛物线 经过直线 与坐标轴的两个交点 .此抛物线与 轴的另一个交点为 .抛物线的顶点为 .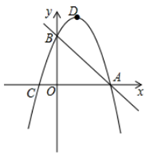 (1)、求此抛物线的解析式;(2)、若点 为抛物线上一动点,是否存在点 .使 与 的面积相等?若存在,求点 的坐标;若不存在,请说明理由.22. 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)、求此抛物线的解析式;(2)、若点 为抛物线上一动点,是否存在点 .使 与 的面积相等?若存在,求点 的坐标;若不存在,请说明理由.22. 如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.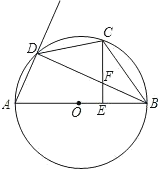 (1)、求证:CF=BF;(2)、若AD=6,⊙O的半径为5,求BC的长.23. 某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
(1)、求证:CF=BF;(2)、若AD=6,⊙O的半径为5,求BC的长.23. 某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
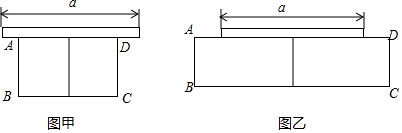 (1)、若a=6.
(1)、若a=6.①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)、若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.24. 如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.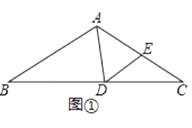
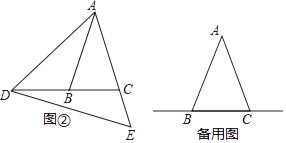
(1)、如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
(2)、如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
(3)、当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.