浙江省天台县2020年数学中考二模试卷
试卷更新日期:2020-05-12 类型:中考模拟
一、单选题
-
1. -8的倒数是( )A、 B、 C、8 D、-82. 下列计算正确的是( )A、 B、 C、 D、3. 如图,是由两个正方体组成的几何体,则该几何体的俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 抛掷一枚质地均匀的硬币,若抛掷95次都是正面朝上,则抛掷第100次正面朝上的概率是( )A、小于 B、等于 C、大于 D、无法确定5. 二次函数 的顶点坐标是( )A、 B、 C、 D、6. 关于x的一元一次不等式3x>6的解都能满足下列哪一个不等式的解( )
4. 抛掷一枚质地均匀的硬币,若抛掷95次都是正面朝上,则抛掷第100次正面朝上的概率是( )A、小于 B、等于 C、大于 D、无法确定5. 二次函数 的顶点坐标是( )A、 B、 C、 D、6. 关于x的一元一次不等式3x>6的解都能满足下列哪一个不等式的解( )
A、4x-9<x B、-3x+2<0 C、2x+4<0 D、7. 如图,AB是⊙O的直径,点C在⊙O上,CD平分∠ACB交⊙O于点D , 若∠ABC=30°,则∠CAD的度数为( )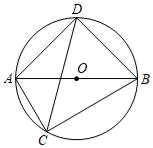 A、100° B、105° C、110° D、1208. 如图,4个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个内角为60°, 、 、 都是格点,则 ( )
A、100° B、105° C、110° D、1208. 如图,4个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个内角为60°, 、 、 都是格点,则 ( ) A、 B、 C、 D、9. 如图, 的半径为2,圆心 在坐标原点,正方形 的边长为2,点 、 在第二象限,点 、 在 上,且点 的坐标为(0,2).现将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合);再将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合),……,按上述方法旋转2020次后,点 的坐标为( )
A、 B、 C、 D、9. 如图, 的半径为2,圆心 在坐标原点,正方形 的边长为2,点 、 在第二象限,点 、 在 上,且点 的坐标为(0,2).现将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合);再将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合),……,按上述方法旋转2020次后,点 的坐标为( )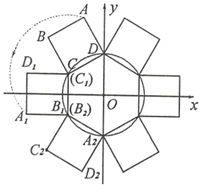 A、(0,2) B、 C、 D、10. 如图,在 中,点 是线段 上一点, ,过点 作 交 的延长线于点 ,若 的面积等于4,则 的面积等于( )
A、(0,2) B、 C、 D、10. 如图,在 中,点 是线段 上一点, ,过点 作 交 的延长线于点 ,若 的面积等于4,则 的面积等于( ) A、8 B、16 C、24 D、32
A、8 B、16 C、24 D、32二、解答题
-
11. 计算: .12. 解方程: = - .13. 如图,在4×4的格点图中, 为格点三角形,即顶点 、 、 均在格点上,利用无刻度直尺按要求完成下列各题,并保留作图痕迹:
 (1)、在边 上找一点 ,使 (请在图①中完成);(2)、在边 上找一点 ,使 (请在图②中完成).14. 某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.
(1)、在边 上找一点 ,使 (请在图①中完成);(2)、在边 上找一点 ,使 (请在图②中完成).14. 某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.抽取的学生最喜欢体育活动的条形统计图
抽取的学生最喜欢体育活动的扇形统计图

请结合以上信息解答下列问题:
(1)、在这次调查中一共抽查了学生,扇形统计图中“乒乓球”所对应的圆心角为度,并请补全条形统计图;(2)、已知该校共有1200名学生,请你估计该校最喜爱跑步的学生人数;(3)、若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组,请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率.15. 已知:如图,在矩形 中,若 ,以 为圆心, 长为半径作 交 的延长线于 ,过 作 ,垂足为 ,且 . (1)、求证: 是 的切线;(2)、求 的长.16. 在平面直角坐标系中,点 , 为反比例函数 上的两个动点,以 , 为顶点构造菱形 .
(1)、求证: 是 的切线;(2)、求 的长.16. 在平面直角坐标系中,点 , 为反比例函数 上的两个动点,以 , 为顶点构造菱形 . (1)、如图1,点 , 横坐标分别为1,4,对角线 轴,菱形 面积为 .求 的值.(2)、如图2,当点 , 运动至某一时刻,点 ,点 恰好落在 轴和 轴正半轴上,此时 .求点 , 的坐标.17. 如图1,抛物线 过点 , ,点 为直线 下方抛物线上一动点, 为抛物线顶点,抛物线对称轴与直线 交于点 .
(1)、如图1,点 , 横坐标分别为1,4,对角线 轴,菱形 面积为 .求 的值.(2)、如图2,当点 , 运动至某一时刻,点 ,点 恰好落在 轴和 轴正半轴上,此时 .求点 , 的坐标.17. 如图1,抛物线 过点 , ,点 为直线 下方抛物线上一动点, 为抛物线顶点,抛物线对称轴与直线 交于点 . (1)、求抛物线的表达式与顶点 的坐标;(2)、在直线 上是否存在点 ,使得 , , , 为顶点的四边形是平行四边形,若存在,请求出 点坐标;(3)、在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.18. 某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中, 、 是 的中线, 于点 ,像 这样的三角形均称为“中垂三角形”.
(1)、求抛物线的表达式与顶点 的坐标;(2)、在直线 上是否存在点 ,使得 , , , 为顶点的四边形是平行四边形,若存在,请求出 点坐标;(3)、在 轴上是否存在点 ,使 ?若存在,求点 的坐标;若不存在,请说明理由.18. 某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中, 、 是 的中线, 于点 ,像 这样的三角形均称为“中垂三角形”.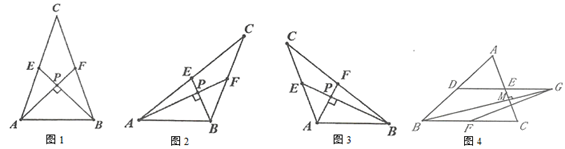 (1)、(特例探究)
(1)、(特例探究)如图1,当 , 时, , ;
如图2,当 , 时, , ;
(2)、(归纳证明)请你观察(1)中的计算结果,猜想 、 、 三者之间的关系,用等式表示出来,并利用图3证明你的结论;
(3)、(拓展证明)如图4,在 中, , , 、 、 分别是边 、 的中点,连结 并延长至 ,使得 ,连结 ,当 于点 时,求 的长.
三、填空题
-
19. 的算术平方根是 ,﹣2的相反数是 ,的绝对值是 .20. 因式分解: .21. 如图,已知等边 的边长为8,以 为直径的 与边 、 分别交于 、 两点,则劣弧 的长为.
 22. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出十二,盈八;人出十,不足六,问人数、物价各几何?译文:今有人合伙购物,每人出12钱,会多8钱;每人出10钱,又会差6钱,问人数、物价各是多少?设合伙人数为 人,物价为 钱,根据题意可列出方程组.23. 为运用数据处理道路拥堵问题,现用流量 (辆/小时)、速度 (千米/小时)、密度 (辆/千米)来描述车流的基本特征.现测得某路段流量 与速度 之间关系的部分数据如下表:
22. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出十二,盈八;人出十,不足六,问人数、物价各几何?译文:今有人合伙购物,每人出12钱,会多8钱;每人出10钱,又会差6钱,问人数、物价各是多少?设合伙人数为 人,物价为 钱,根据题意可列出方程组.23. 为运用数据处理道路拥堵问题,现用流量 (辆/小时)、速度 (千米/小时)、密度 (辆/千米)来描述车流的基本特征.现测得某路段流量 与速度 之间关系的部分数据如下表:速度 (千米/小时)
……
15
20
32
40
45
……
流量 (辆/小时)
……
1050
1200
1152
800
450
……
若已知 、 满足形如 ( 、 为常数)的二次函数关系式,且 、 、 满足 .根据监控平台显示,当 时,道路出现轻度拥堵,试求此时密度 的取值范围是.
24. 在滑草过程中,小明发现滑道两边形如两条双曲线.如图,点 , , …在反比例函数 的图象上,点 , , …在反比例函数 的图象上, 轴,已知点 , …的横坐标分别为1,2…,令四边形 、 、…的面积分别为 、 、…, (1)、用含 的代数式表示 ;(2)、若 ,则 .
(1)、用含 的代数式表示 ;(2)、若 ,则 .