江苏省无锡市滨湖区2020年数学中考模拟试卷(3月)
试卷更新日期:2020-05-12 类型:中考模拟
一、单选题
-
1. 9的算术平方根是( )A、-3 B、3 C、 D、±32. 下列运算正确的是( )A、a3•a2=a6 B、a7÷a3=a4 C、(﹣3a)2 =﹣6a2 D、(a﹣1)2=a2﹣13. 下列各数中,属于无理数的是 ( )A、-2 B、0 C、 D、0.1010010004. 函数 y= 中自变量x的取值范围为( )A、x>2 B、x≥2 C、x<2 D、x≤25. 关于x的一元二次方程 的两实数根分别为 、 ,且 ,则m的值为( )A、 B、 C、 D、06. 如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
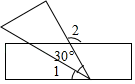 A、48° B、78° C、92° D、102°7. 若一元二次方程x2﹣2kx+k2=0的一根为x=﹣1,则k的值为( )A、﹣1 B、0 C、1或﹣1 D、2或08. 已知直角三角形的外接圆半径为6,内切圆半径为2,那么这个三角形的面积是( )A、32 B、34 C、27 D、289. 在同一平面直角坐标系中,函数y=﹣x+k与y= (k为常数,且k≠0)的图象大致是( )A、
A、48° B、78° C、92° D、102°7. 若一元二次方程x2﹣2kx+k2=0的一根为x=﹣1,则k的值为( )A、﹣1 B、0 C、1或﹣1 D、2或08. 已知直角三角形的外接圆半径为6,内切圆半径为2,那么这个三角形的面积是( )A、32 B、34 C、27 D、289. 在同一平面直角坐标系中,函数y=﹣x+k与y= (k为常数,且k≠0)的图象大致是( )A、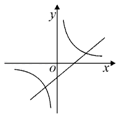 B、
B、 C、
C、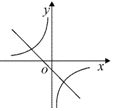 D、
D、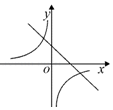 10. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( )
10. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 函数y= 的自变量x的取值范围是.12. 因式分解:2m2-8m+8=.13. 在根式 , , , 中随机抽取一个,它是最简二次根式的概率为.14. 据统计,2019年全国高考人数再次突破千万,高达10310000人.数据10310000用科学记数法可表示为人.15. 已知一个多边形的内角和是外角和的
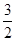 ,则这个多边形的边数是. 16. 圆锥的底面半径为14 cm,母线长为21 cm,则该圆锥的侧面展开图的圆心角为度.17. 如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=°.
,则这个多边形的边数是. 16. 圆锥的底面半径为14 cm,母线长为21 cm,则该圆锥的侧面展开图的圆心角为度.17. 如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=°.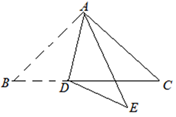 18. 如图,将半径为6的半圆,绕点A逆时针旋转60°,使点B落到点B′处,则图中阴影部分的面积是.
18. 如图,将半径为6的半圆,绕点A逆时针旋转60°,使点B落到点B′处,则图中阴影部分的面积是. 19. 如图,正比例函数y1=k1x的图象与反比例函数y2= (x>0)的图象相交于点A( ,2 ),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是.
19. 如图,正比例函数y1=k1x的图象与反比例函数y2= (x>0)的图象相交于点A( ,2 ),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是.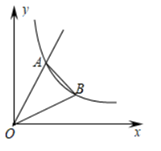 20. 如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接GF并延长,交AC的延长线于点P,若AB=5,CF=2,则线段EP的长是.
20. 如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接GF并延长,交AC的延长线于点P,若AB=5,CF=2,则线段EP的长是.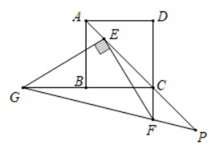
三、解答题
-
21.(1)、计算:(﹣3)2﹣(π﹣4)0+( )﹣2;(2)、(a+2)2+(1﹣a)(1+a).(3)、解方程: = ;(4)、解不等式组:22. 化简: ÷ ,当a= ,b= 时,求出这个代数式的值.23. 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)
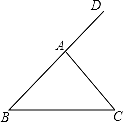 (1)、作∠DAC的平分线AM;(2)、作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF
(1)、作∠DAC的平分线AM;(2)、作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF探究与猜想:若∠BAE=36°,求∠B的度数.
24. 如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.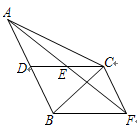 (1)、求证:CF=AD;(2)、若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.25. 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)、求证:CF=AD;(2)、若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.25. 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E. (1)、求证:AC∥DE;(2)、连接CD,若OA=AE=2时,求出四边形ACDE的面积.26. 某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
(1)、求证:AC∥DE;(2)、连接CD,若OA=AE=2时,求出四边形ACDE的面积.26. 某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
(利润=(销售价-进价)
 销售量)(1)、请根据他们的对话填写下表:
销售量)(1)、请根据他们的对话填写下表:销售单价x(元/kg)
10
11
13
销售量y(kg)
(2)、请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;(3)、设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?27. 如图,在平面直角坐标系中,直线y=﹣ x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.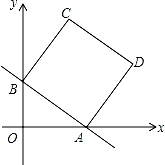 (1)、填空:b=;(2)、求点D的坐标;(3)、点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.28. 已知二次函数 >0)的对称轴与x轴交于点B,与直线l: 交于点C,点A是该二次函数图象与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
(1)、填空:b=;(2)、求点D的坐标;(3)、点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.28. 已知二次函数 >0)的对称轴与x轴交于点B,与直线l: 交于点C,点A是该二次函数图象与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2. (1)、求抛物线的函数关系式;(2)、若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
(1)、求抛物线的函数关系式;(2)、若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.