江苏省无锡市2020年初中毕业升学预测数学试卷
试卷更新日期:2020-05-12 类型:中考模拟
一、单选题
-
1. 下列等式正确的是( )A、 B、 C、 D、2. 函数 中自变量x的取值范围是( )A、x< B、x≥ C、x≤ D、x>3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图案中,既是轴对称图形又是中心对称图形的有( )
 A、1个 B、2个 C、3个 D、4个5. 在一次考试中,某小组6名同学的成绩(单位:分)分别是:7、9、9、8、7、7,则这组数据的众数和中位数是( )A、7、7.5 B、7、7 C、7、8 D、7、8.56. 已知一次函数 经过P(a,b),则 的值为( )A、1 B、 C、2 D、7. 下列性质中,矩形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、4个内角相等 D、一条对角线平分一组对角8. 小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )
A、1个 B、2个 C、3个 D、4个5. 在一次考试中,某小组6名同学的成绩(单位:分)分别是:7、9、9、8、7、7,则这组数据的众数和中位数是( )A、7、7.5 B、7、7 C、7、8 D、7、8.56. 已知一次函数 经过P(a,b),则 的值为( )A、1 B、 C、2 D、7. 下列性质中,矩形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、4个内角相等 D、一条对角线平分一组对角8. 小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )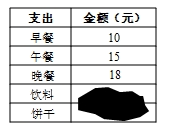 A、4 B、15 C、22 D、449. 如图, 的三个顶点 均在 上,且对角线 经过点 , 与 相切于点 ,已知 的半径为6,则 的面积为( ).
A、4 B、15 C、22 D、449. 如图, 的三个顶点 均在 上,且对角线 经过点 , 与 相切于点 ,已知 的半径为6,则 的面积为( ). A、35 B、 C、 D、10. 如图是由4个边长为a的正六边形组成的网格图,每个顶点均为格点,若该图中到点A的距离超过3的格点有且仅有6个,则a的取值范围为( )
A、35 B、 C、 D、10. 如图是由4个边长为a的正六边形组成的网格图,每个顶点均为格点,若该图中到点A的距离超过3的格点有且仅有6个,则a的取值范围为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 已知无锡市总面积约为4787000000 ,用科学记数法表示这个数为.13. 计算:sin30°+cos45°=.14. 命题“如果a2=b2 , 那么a=b”的逆命题是命题.(填写“真”或“假”)15. 已知圆锥的底面直径为6,高为4,则该圆锥的侧面积为.16. 已知10个初三学生的数学中考成绩分布如右表所示,则这10个学生的平均分为.
分数段
平均分
人数
120以上
126
1
110-120
114
100-110
106
5
100以下
96
2
17. 如图,矩形 , , 的4个顶点都落在矩形边上,且有 ,设 的面积为 ,矩形 的面积为 ,则 的最大值为. 18. 如图,等腰 , , ,点 为 上一点,且 ,连接 ,将 沿 翻折得到 ,连接 ,则 的长为.
18. 如图,等腰 , , ,点 为 上一点,且 ,连接 ,将 沿 翻折得到 ,连接 ,则 的长为.
三、解答题
-
19.(1)、 ;(2)、 .20.(1)、解方程:(2)、解不等式:21. 已知,如图,矩形ABCD中,点E、F均为BC边上的点,且满足BE=CF,连接AE、DF,延长相交于点G,求证:AG=DG.
 22. 本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
22. 本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
根据统计图解答下列问题:
(1)、本次测试的学生中,得4分的学生有多少人?(2)、本次测试的平均分是多少分?(3)、通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?23. 周末,小明与小亮两个人打算骑共享单车骑行出游,两人打开手机APP进行选择,已知附近共有3种品牌的5辆车,其中A品牌与B品牌各有2辆,C品牌有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.(1)、若小明首先选择,则小明选中A品牌单车的概率为;(2)、求小明和小亮选中同一品牌单车的概率.(请用“画树状图”或“列表”的方法给出分析过程)24. 某企业生产的一种果汁饮料由A、B两种水果配制而成,其比例与成本如下方表格所示,已知该饮料的成本价为8元/千克,按现价售出后可获利润50%,每个月可出售27500瓶.每千克饮料所占比例
成本(元/千克)
A
20%
m
B
80%
m-15
(1)、求m的值;(2)、由于物价上涨,A水果成本提高了25%,B水果成本提高了20%,在不改变售价的情况下,若要保持每个月的利润不减少,则现在至少需要售出多少瓶饮料?25. 如图,在直角坐标系内,已知 ,直线 过 , 、 关于 的对称点分别为 ,请利用直尺(无刻度)和圆规按下列要求作图. (1)、当 与 重合时,请在图 中画出点 位置,并求出 的值;(2)、当 都落在 轴上时,请在图2中画出直线 ,并求出 的值.26. 在直角坐标系中,已知抛物线 (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知 :S四边形ACBD=1:4.
(1)、当 与 重合时,请在图 中画出点 位置,并求出 的值;(2)、当 都落在 轴上时,请在图2中画出直线 ,并求出 的值.26. 在直角坐标系中,已知抛物线 (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知 :S四边形ACBD=1:4. (1)、求点D的坐标(用仅含a、c的代数式表示);(2)、若tan∠ACB= ,求抛物线的解析式.27. 如图,已知 , , ,将 绕点 逆时针旋转,得到 ,点 在 延长线上
(1)、求点D的坐标(用仅含a、c的代数式表示);(2)、若tan∠ACB= ,求抛物线的解析式.27. 如图,已知 , , ,将 绕点 逆时针旋转,得到 ,点 在 延长线上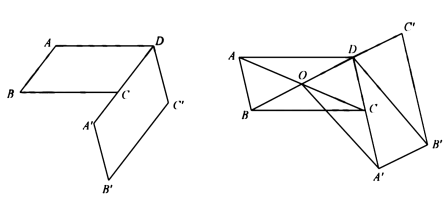 (1)、若 ,当 所在直线恰好经过点 时,求点 运动到 所经过的路径的长度:(2)、连接 相交于点 ,连接 ,当四边形 为平行四边形时,求 的值.28. 已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.
(1)、若 ,当 所在直线恰好经过点 时,求点 运动到 所经过的路径的长度:(2)、连接 相交于点 ,连接 ,当四边形 为平行四边形时,求 的值.28. 已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.
现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率= ×100%)
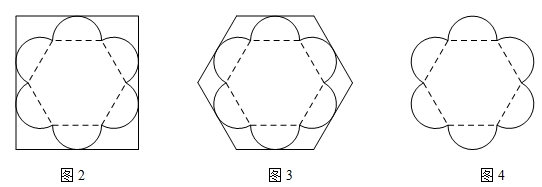 (1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
(1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.