江苏省苏州市吴江市2020年数学中考模拟试卷
试卷更新日期:2020-05-12 类型:中考模拟
一、单选题
-
1. 如图,数轴上的点A表示的数为a,则a的相反数等于( )
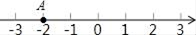 A、﹣2 B、2 C、 D、2. 下列运算正确的是( )A、a2+a3=a5 B、(a+b)2=a2+b2 C、(a2)3=a5 D、x2•x3=x53. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A、﹣2 B、2 C、 D、2. 下列运算正确的是( )A、a2+a3=a5 B、(a+b)2=a2+b2 C、(a2)3=a5 D、x2•x3=x53. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A、30° B、40° C、50° D、60°4. 二次函数 y=(x﹣4)2+3 的最小值是( )A、2 B、3 C、4 D、55. 下列图形中,即是轴对称图形又是中心对称图形的是( )A、 B、
B、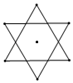 C、
C、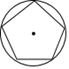 D、
D、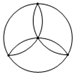 6. 对于两组数据A,B,如果sA2>sB2 , 且 ,则( )A、这两组数据的波动相同 B、数据B的波动小一些 C、它们的平均水平不相同 D、数据A的波动小一些7. 轮船沿江从 港顺流行驶到 港,比从 港返回 港少用3小时,若船速为26千米/时,水速为2千米/时,求 港和 港相距多少千米. 设 港和 港相距 千米. 根据题意,可列出的方程是( ).A、 B、 C、 D、8. 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )
6. 对于两组数据A,B,如果sA2>sB2 , 且 ,则( )A、这两组数据的波动相同 B、数据B的波动小一些 C、它们的平均水平不相同 D、数据A的波动小一些7. 轮船沿江从 港顺流行驶到 港,比从 港返回 港少用3小时,若船速为26千米/时,水速为2千米/时,求 港和 港相距多少千米. 设 港和 港相距 千米. 根据题意,可列出的方程是( ).A、 B、 C、 D、8. 如图,A、B是边长为1的小正方形组成的网格上的两个格点,在格点中任意放置点C,恰好能使△ABC的面积为1的概率是( )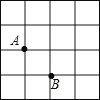 A、 B、 C、 D、9. 如图,等边三角形 内接于 ,若 的半径为2,则图中阴影部分的面积等于( )
A、 B、 C、 D、9. 如图,等边三角形 内接于 ,若 的半径为2,则图中阴影部分的面积等于( ) A、 B、 C、 D、10. 如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2),设AE=x(0<x<2),给出下列判断:①x= 时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
A、 B、 C、 D、10. 如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2),设AE=x(0<x<2),给出下列判断:①x= 时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )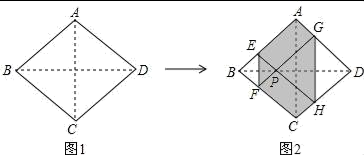 A、①② B、①③ C、② D、②③
A、①② B、①③ C、② D、②③二、填空题
-
11. 已知关于 的方程 两个根是互为相反数,则 的值为.12. 舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为 .13. 如果把抛物线y=2x2﹣1向左平移1个单位,同时向上平移4个单位,那么得到的新的抛物线是.14. 分式方程 的解是 .15. 如图,O为Rt△ABC斜边中点,AB=10,BC=6,M,N在AC边上,∠MON=∠B,若△OMN与△OBC相似,则CM=.
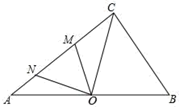 16. 如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为.
16. 如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为.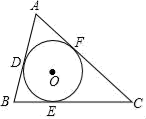 17. 如图,在边长为3正方形ABCD的外部作Rt△AEF,且AE=AF=1,连接DE,BF,BD,则DE2+BF2=.
17. 如图,在边长为3正方形ABCD的外部作Rt△AEF,且AE=AF=1,连接DE,BF,BD,则DE2+BF2=.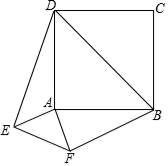 18. 如图,点 是双曲线 在第二象限分支上的一个动点,连接 并延长交另一分支于点 ,以 为底作等腰 ,且 ,点 在第一象限,随着点 的运动点 的位置也不断变化,但点 始终在双曲线 上运动,则 的值为.
18. 如图,点 是双曲线 在第二象限分支上的一个动点,连接 并延长交另一分支于点 ,以 为底作等腰 ,且 ,点 在第一象限,随着点 的运动点 的位置也不断变化,但点 始终在双曲线 上运动,则 的值为.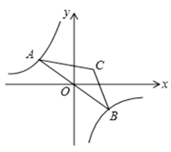
三、解答题
-
19. 计算: +tan60°-(sin45°)-1-|1- |20. 关于x、y的方程组 的解满足x大于0,y小于4.求a的取值范围.21. 先化简 ,然后从﹣1,0,2中选一个合适的x的值,代入求值。22. 为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
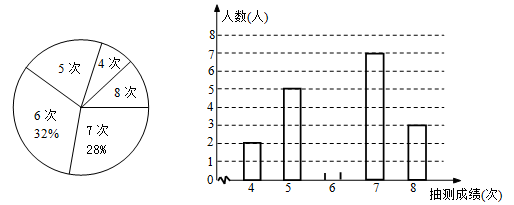 (1)、本次抽测的男生有人,抽测成绩的众数是;(2)、请将条形图补充完整;(3)、若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
(1)、本次抽测的男生有人,抽测成绩的众数是;(2)、请将条形图补充完整;(3)、若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
23. 小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)、计算“3点朝上”的频率和“5点朝上”的频率.(2)、小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?24. 如图,在等腰Rt△ABC中,∠C=90°,AC=4,矩形DEFG的顶点D、G分别在AC、BC上,边EF在AB上. (1)、求证:△AED∽△DCG;(2)、若矩形DEFG的面积为4,求AE的长.25. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:
(1)、求证:△AED∽△DCG;(2)、若矩形DEFG的面积为4,求AE的长.25. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:x/元
…
15
20
25
…
y/件
…
25
20
15
…
已知日销售量y是销售价x的一次函数.
(1)、求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;(2)、当每件产品的销售价定为35元时,此时每日的销售利润是多少元?26. 如图,AB为⊙O的直径,且AB=m(m为常数),点C为 的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P , 弦CD交AB于点E . (1)、当DC⊥AB时,则 =;(2)、①当点D在 上移动时,试探究线段DA , DB , DC之间的数量关系;并说明理由;
(1)、当DC⊥AB时,则 =;(2)、①当点D在 上移动时,试探究线段DA , DB , DC之间的数量关系;并说明理由;②设CD长为t , 求△ADB的面积S与t的函数关系式;
(3)、当 时,求 的值.27. 如图,直线L:y=﹣ x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.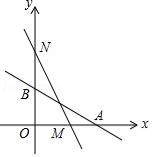 (1)、点A的坐标:;点B的坐标:;(2)、求△NOM的面积S与M的移动时间t之间的函数关系式;(3)、在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;(4)、在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.28. 如图,抛物线y=mx2﹣4mx+2m+1与x轴交于A(x1 , 0),B(x2 , 0)两点,与y轴交于点C,且x2﹣x1=2.
(1)、点A的坐标:;点B的坐标:;(2)、求△NOM的面积S与M的移动时间t之间的函数关系式;(3)、在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;(4)、在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.28. 如图,抛物线y=mx2﹣4mx+2m+1与x轴交于A(x1 , 0),B(x2 , 0)两点,与y轴交于点C,且x2﹣x1=2.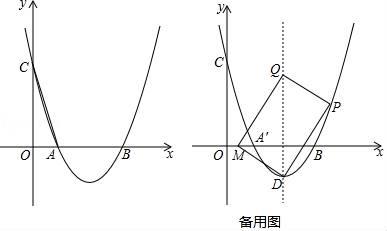 (1)、求抛物线的解析式;(2)、E是抛物线上一点,∠EAB=2∠OCA,求点E的坐标;(3)、设抛物线的顶点为D,动点P从点B出发,沿抛物线向上运动,连接PD,过点P做PQ⊥PD,交抛物线的对称轴于点Q,以QD为对角线作矩形PQMD,当点P运动至点(5,t)时,求线段DM扫过的图形面积.
(1)、求抛物线的解析式;(2)、E是抛物线上一点,∠EAB=2∠OCA,求点E的坐标;(3)、设抛物线的顶点为D,动点P从点B出发,沿抛物线向上运动,连接PD,过点P做PQ⊥PD,交抛物线的对称轴于点Q,以QD为对角线作矩形PQMD,当点P运动至点(5,t)时,求线段DM扫过的图形面积.