江苏省南京市鼓楼区2020年数学中考模拟试卷

试卷更新日期：2020-05-12 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，点A所表示的数的绝对值是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 共享单车的投放使用为人们的工作和生活带来了极大的便利，不仅有效缓解了出行“最后一公里”问题，而且经济环保，据相关部门2018年11月统计数据显示，郑州市互联网租赁自行车累计投放超过49万辆，将49万用科学记数法表示正确的是（）

A、4.9×10⁴ B、4.9×10⁵ C、0.49×10⁴ D、49×10⁴

查看试题解析
3. 计算（﹣x²）³的结果是（）

A、﹣x⁶ B、x⁶ C、﹣x⁵ D、﹣x⁸

查看试题解析
4. 如图，为了美化校园，学校在一块边角空地建造了一个扇形花圃，扇形圆心角∠AOB＝120°，半径OA为9m，那么花圃的面积为（）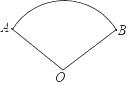

A、54πm² B、27πm² C、18πm² D、9πm²

查看试题解析
5. 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：

衬衫尺码

39

40

41

42

43

平均每天销售件数

10

12

20

12

12

该店主决定本周进货时，增加一些41码的衬衫，影响该店主决策的统计量是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
6. 小刚去距县城28千米的旅游点游玩，先乘车，后步行．全程共用了1小时，已知汽车速度为每小时36千米，步行的速度每小时4千米，则小刚乘车路程和步行路程分别是（　　）

A、26千米，2千米 B、27千米，1千米 C、25千米，3千米 D、24千米，4千米

查看试题解析

二、填空题

7. 若|﹣x|＝5，则x＝.

查看试题解析
8. 袋中装有6个黑球和n个白球，经过若干次试验，发现“若从袋中任摸出一个球，恰是黑球的概率为 $\frac{3}{4}$ ，则这个袋中白球大约有个．

查看试题解析
9. 若一个多边形的内角和比外角和大360°，则这个多边形的边数为．

查看试题解析
10. 方程 $\frac{1}{x + 2} = \frac{2}{x}$ 的解是.

查看试题解析
11. 分解因式：4m²﹣16n²＝．

查看试题解析
12. 已知直线 y=ax（a≠0）与反比例函数 y= $\frac{k}{x}$ （k≠0）的图象一个交点坐标为（2，4），则它们另一个交点的坐标是．

查看试题解析
13. 如图，四边形ABCD内接于圆O，AD∥BC，∠DAB=48°，则∠AOC的度数是.

查看试题解析
14. 某市规定了每月用水不超过l8立方米和超过18立方米两种不同的收费标准，该市用户每月应交水费y（元）是用水x（立方米）的函数，其图象如图所示.已知小丽家3月份交了水费102元，则小丽家这个月用水量为立方米.

查看试题解析
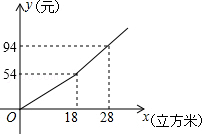15. 如图，正方形ABCD中， $AB = 9$ ，点E在边CD上，且 $CD = 3 DE .$ 将 $△ ADE$ 沿AE对折至 $△ AFE$ ，延长EF交边BC于点G，连接AG、 $CF .$ 则 $△ FGC$ 的面积是.

查看试题解析
16. 如图，在平面直角坐标系xOy中，直线 $y = \sqrt{3} x$ 经过点A，作AB⊥x轴于点B，将△ABO绕点B逆时针旋转60°，得到△CBD，若点B的坐标为（4，0），则点C的坐标为.

查看试题解析

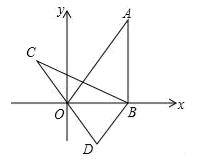
三、解答题

17. 计算：2sin30°﹣（π﹣ $\sqrt{2}$ ）⁰+| $\sqrt{3}$ ﹣1|+（ $\frac{1}{2}$ ）^﹣¹

查看试题解析
18. 计算 $\frac{a - 2}{a - 1} \div (a + 1 - \frac{3}{a - 1})$

查看试题解析
19. 解不等式（组）

(1)、 ${\begin{array}{l} 2 x + 3 > 5 \\ 3 x - 2 < 4 \end{array}$

(2)、 ${\begin{array}{l} 2 x - 1 \geq x + 1 \\ x + 8 \leq 4 x - 1 \end{array}$

查看试题解析
20. 如图，在平行四边形ABCD中，E，F为对角线BD上的两点，且∠DAE＝∠BCF.

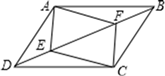
求证：

(1)、AE＝CF；

(2)、四边形AECF是平行四边形.

查看试题解析
21. 小昕的口袋中有5把相似的钥匙，其中2把钥匙（记为A₁ ， A₂）能打开教室前门锁，而剩余的3把钥匙（记为B₁ ， B₂ ， B₃）不能打开教室前门锁.

(1)、小昕从口袋中随便摸出一把钥匙就能打开教室前门锁的概率是；

(2)、请用树状图或列表等方法，求出小昕从口袋中第一次随机摸出的一把钥匙不能打开教室前门锁（摸出的钥匙不再放回），而第二次随机摸出的一把钥匙正好能打开教室前门锁的概率.

查看试题解析
22. 某种新商品每件进价是120元，在试销期间发现，当每件商品售价为130元时，每天可销售70件，当每件商品售价高于130元时，每涨价1元，日销售量就减少1件．据此规律，请回答：

(1)、当每件商品售价定为170元时，每天可销售多少件商品商场获得的日盈利是多少？

(2)、在商品销售正常的情况下，每件商品的涨价为多少元时，商场日盈利最大？最大利润是多少？

查看试题解析
23. 如图，在平面直角坐标系中，函数y=2x+8的图象分别交x轴、y轴于A、B两点，过点A的直线交y轴正半轴于点M，且点M为线段OB的中点.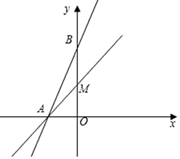

(1)、求直线AM的函数解析式.

(2)、试在直线AM上找一点P，使得S_△_ABP=S_△_AOB ，求出点P的坐标.

(3)、若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、B、M、H为顶点的四边形是平行四边形？若存在，请直接写出所有点H的坐标；若不存在，请说明理由.

查看试题解析
24. 如图，在△ABC中，∠BAC=45°，AD⊥BC于点D，BD=6，DC=4，求AD的长.小明同学利用翻折，巧妙地解答了此题，按小明的思路探究并解答下列问题：

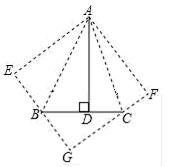(1)、分别以AB，AC所在直线为对称轴，画出△ABD和△ACD的对称图形，点D的对称点分别为点E，F，延长EB和FC相交于点G，求证：四边形AEGF是正方形；

(2)、设AD=x，建立关于x的方程模型，求出AD的长.

查看试题解析
25. 自2017年3月起，成都市中心城区居民用水实行以户为单位的三级阶梯收费办法：
第I级：居民每户每月用水18吨以内含18吨每吨收水费a元；

第Ⅱ级：居民每户每月用水超过18吨但不超过25吨，未超过18吨的部分按照第Ⅰ级标准收费，超过部分每吨收水费b元；

第Ⅲ级：居民每户每月用水超过25吨，未超过25吨的部分按照第I、Ⅱ级标准收费，超过部分每吨收水费c元.

设一户居民月用水x吨，应缴水费为y元，y与x之间的函数关系如图所示

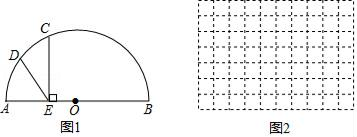
(1)、根据图象直接作答：a＝， b＝；

(2)、求当x≥25时y与x之间的函数关系；

(3)、把上述水费阶梯收费办法称为方案①，假设还存在方案②：居民每户月用水一律按照每吨4元的标准缴费，请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.（写出过程）

查看试题解析

26. 如图1，AB为半圆O的直径，半径的长为4cm，点C为半圆上一动点，过点C作CE⊥AB，垂足为点E，点D为弧AC的中点，连接DE，如果DE=2OE，求线段AE的长.

小何根据学习函数的经验，将此问题转化为函数问题解决.

小华假设AE的长度为xcm，线段DE的长度为ycm.

（当点C与点A重合时，AE的长度为0cm），对函数y随自变量x的变化而变化的规律进行探究.

下面是小何的探究过程，请补充完整：（说明：相关数据保留一位小数）.

(1)、通过取点、画图、测量，得到了x与y的几组值，如下表：

x/cm	0	1	2	3	4	5	6	7	8
y/cm	0	1.6	2.5	3.3	4.0	4.7		5.8	5.7

当x=6cm时，请你在图中帮助小何完成作图，并使用刻度尺度量此时线段DE的长度，填写在表格空白处：

(2)、在图2中建立平面直角坐标系，描出补全后的表中各组对应值为坐标的点，画出该函数的图象；

(3)、结合画出的函数图象解决问题，当DE=2OE时，AE的长度约为cm.

查看试题解析

27. 如图，在平面直角坐标系中，直线y＝kx﹣4k+4与抛物线y＝ $\frac{1}{4}$ x²﹣x交于A、B两点.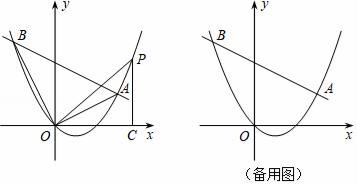

(1)、直线总经过定点，请直接写出该定点的坐标；

(2)、点P在抛物线上，当k＝﹣ $\frac{1}{2}$ 时，解决下列问题：
①在直线AB下方的抛物线上求点P，使得△PAB的面积等于20；

②连接OA，OB，OP，作PC⊥x轴于点C，若△POC和△ABO相似，请直接写出点P的坐标.

查看试题解析

衬衫尺码	39	40	41	42	43
平均每天销售件数	10	12	20	12	12