湖北省宜昌市2020年数学中考模拟试卷

试卷更新日期：2020-05-12 类型：中考模拟

进入出卷网下载

一、单选题

1. 若∣－a∣＝a，则a的取值范围是（）

A、a<0 B、a>0 C、a≥0 D、a≤0

查看试题解析
2. 下列运算正确的是（）

A、a³•a⁴＝a¹² B、（a³）²＝a⁵ C、（3a²）³＝27a⁶ D、a⁶÷a³＝a²

查看试题解析
3. 已知 $x > y$ ，则下列不等式不成立的是（）

A、 $x - 6 > y - 6$ B、 $3 x > 3 y$ C、 $- 2 x < - 2 y$ D、 $- 3 x + 6 > - 3 y + 6$

查看试题解析
4. 化简 $\frac{1}{x y - y^{2}} + \frac{x + y}{x^{2} - y^{2}}$ 的结果是（）

A、 $\frac{1}{y (x - y)}$ B、 $\frac{y + 1}{y (x - y)}$ C、 $\frac{y - 1}{y (x - y)}$ D、 $\frac{1}{y (x + y)}$

查看试题解析
5. 如果点P（-2，b）和点Q（a，-3）关于x轴对称，则 $a + b$ 的值是（）

A、1 B、-1 C、5 D、-5

查看试题解析
6. 数据4，3，5，3，6，3，4的众数和中位数是（）

A、3，4 B、3，5 C、4，3 D、4，5

查看试题解析
7. 已知二次函数y＝ax²＋bx＋c(a≠0)的图象如图所示，当y＞0时，x的取值范围是（）

A、－1＜x＜2 B、x＞2 C、x＜－1 D、x＜－1或x＞2

查看试题解析
8. 港珠澳大桥2018年10月24日上午9时正式通车，这座大桥跨越伶仃洋，东接香港，西接广东珠海和澳门，总长约55000m，集桥、岛、隧于一体，是世界最长的跨海大桥，数据55000用科学记数法表示为（）

A、5.5×10⁵ B、55×10⁴ C、5.5×10⁴ D、5.5×10⁶

查看试题解析
9. 某商场试销一种新款衬衫，一周内售出型号记录情况如表所示：
型号（厘米）
38
39
40
41
42
43
数量（件）
25
30
36
50
28
8
商场经理要了解哪种型号最畅销，则上述数据的统计量中，对商场经理来说最有意义的是（　　）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
10. 将矩形OABC如图放置，O为原点，若点A的坐标是（﹣1，2），点B的坐标是（2， $\frac{7}{2}$ ），则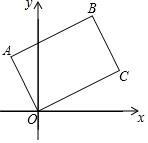点C的坐标是（）

A、（4，2） B、（2，4） C、（ $\frac{3}{2}$ ，3） D、（3， $\frac{3}{2}$ ）

查看试题解析
11. 已知直线l及直线l外一点P.如图，（1）在直线l上取一点O，以点O为圆心，OP长为半径画半圆，交直线l于A，B两点；（2）连接PA，以点B为圆心，AP长为半径画弧，交半圆于点Q；（3）作直线PQ，连接BP.根据以上作图过程及所作图形，下列结论中错误的是（）

A、AP＝BQ B、PQ∥AB C、∠ABP＝∠PBQ D、∠APQ+∠ABQ＝180°

查看试题解析

二、填空题

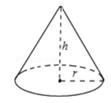
12. 已知m是方程式x²+x﹣1＝0的根，则式子m³+2m²+2019的值为.

查看试题解析
13. 如图，圆锥的底面半径r为6cm，高h为8cm，则圆锥的侧面积为。

查看试题解析
14. 如图，四边形ABCD为⊙O的内接四边形，已知∠BOD= 100°，则∠BCD=.

查看试题解析
15. 如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF=12，CF=3，则AC =.

查看试题解析

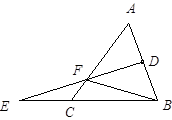
三、解答题

16. 解方程或不等式（组）：

(1)、 ${\begin{array}{l} y = 2 x - 3 \\ 3 x + 2 y = 8 \end{array}$

(2)、 $\frac{x + 6}{2} < - \frac{2 x + 1}{3}$ ；

查看试题解析
17. 先化简，再求值： $(x + 2 - \frac{5}{x - 2}) \div \frac{x - 3}{3 x^{2} - 6 x}$ ，其中 $x$ 满足 $x^{2} + 3 x - 1 = 0$ .

查看试题解析
18. 如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N.

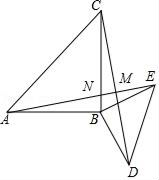(1)、求证：AE＝CD；

(2)、求证：AE⊥CD；

(3)、连接BM，有以下两个结论：①BM平分∠CBE；②MB平分∠AMD.其中正确的有（请写序号，少选、错选均不得分）.

查看试题解析
19. 在⊙O中，AB为直径，C为⊙O上一点.

(1)、如图①，过点C作⊙O的切线，与AB的延长线相交于点P，若∠CAB＝32°，求∠P的大小；

(2)、如图②，D为优弧ADC上一点，且DO的延长线经过AC的中点E，连接DC与AB相交于点P，若∠CAB＝16°，求∠DPA的大小.

查看试题解析
20. 为了了解班级学生数学课前预习的具体情况，郑老师对本班部分学生进行了为期一个月的跟踪调查，他将调查结果分为四类：A：很好；B：较好；C：一般；D：不达标，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：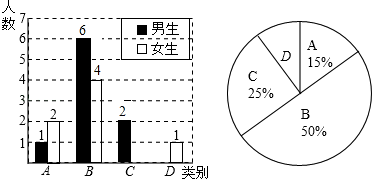

(1)、C类女生有名，D类男生有名，将上面条形统计图补充完整；

(2)、扇形统计图中“课前预习不达标”对应的圆心角度数是；

(3)、为了共同进步，郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习，请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率，

查看试题解析
21. 如图，一次函数y₁＝﹣x﹣1的图象与x轴交于点A，与y轴交于点B，与反比例函数 $y_{2} = \frac{k}{x}$ 图象的一个交点为M（﹣2，m）.

(1)、求反比例函数的解析式；

(2)、当y₂＞y₁时，求x的取值范围；

(3)、求点B到直线OM的距离.

查看试题解析
22. 红灯笼，象征着阖家团圆，红红火火，挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼，用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同，已知乙灯笼每对进价比甲灯笼每对进价多9元.

(1)、求甲、乙两种灯笼每对的进价；

(2)、经市场调查发现，乙灯笼每对售价50元时，每天可售出98对，售价每提高1元，则每天少售出2对：物价部门规定其销售单价不高于每对65元，设乙灯笼每对涨价x元，小明一天通过乙灯笼获得利润y元.
①求出y与x之间的函数解析式；

②乙种灯笼的销售单价为多少元时，一天获得利润最大？最大利润是多少元？

查看试题解析
23. 在△ABC中，∠ABC＝120°，线段AC绕点C顺时针旋转60°得到线段CD ，连接BD ．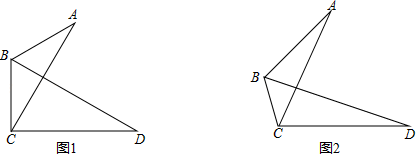

(1)、如图1，若AB＝BC ，求证：BD平分∠ABC；

(2)、如图2，若AB＝2BC ，
①求 $\frac{B D}{A C}$ 的值；

查看试题解析
24. 如图，直线y＝- $\frac{1}{2}$ x-3与x轴，y轴分别交于点A，C，经过点A，C的抛物线y＝ax²+bx﹣3与x轴的另一个交点为点B(2，0)，点D是抛物线上一点，过点D作DE⊥x轴于点E，连接AD，DC.设点D的横坐标为m.

(1)、求抛物线的解析式；

(2)、当点D在第三象限，设△DAC的面积为S，求S与m的函数关系式，并求出S的最大值及此时点D的坐标；

(3)、连接BC，若∠EAD＝∠OBC，请直接写出此时点D的坐标.

查看试题解析

型号（厘米）	38	39	40	41	42	43
数量（件）	25	30	36	50	28	8