河南省周口市2020年数学中考模拟试卷
试卷更新日期：2020-05-12 类型：中考模拟
一、单选题
-
1. 下列四个数中最大的数是（ ）A、﹣ B、﹣0.5 C、- D、-π2. 2019 年 11 月 20 日至 23 日，首届“世界 5G大会“在中国亦庄举办，据悉，在未来 5 年，5G的商业产值或超过 35 万亿元人民币，35 万亿用科学记数法表示为（ ）A、 35×1012 B、3.5×1012 C、3.5×1013 D、0.35×10143. 下列几何体中，主视图和俯视图相同的是（ ）A、
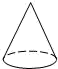B、
C、
D、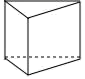
4.如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（ ）
A、 B、 C、 D、5. 下列说法正确的是（ ）A、一个游戏中奖的概率是 ，则做100次这样的游戏一定会中奖 B、为了了解全国中学生的心理健康状况，应采用普查的方式 C、一组数据0，1，2，1，1的众数和中位数都是1 D、若甲组数据的方差S甲2=0.2，乙组数据的方差S乙2=0.5，则乙组数据比甲组数据稳定6. 如图，将矩形A B C D 沿 GH 折叠，点C 路在点 Q 处，点 D落在 AB 边上的点 E处，若∠AG E＝34°.则∠BH Q 等于（ ）
A、73° B、34° C、45° D、30°7. 已知二次函数 的图象开口向下，且与 x轴的负半轴交于点 P，则一次函数 的图象经过的象限是（ ）A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限8. 如图， 内接于⊙ ， ，则 的度数为（ ）
A、110° B、115° C、120° D、125°9. 如图，在平面直角坐标系中，四边形 ABCD是菱形，BC∥x 轴.AD 与 y轴交于点 E，反比例函数 y＝ （x＞0）的图象经过顶点 C、D，已知点 C的横坐标为5，BE＝2DE，则 k的值为（ ）
A、 B、 C、 D、510. 如图，已知菱形 A，B，C，D 的顶点 A（0，﹣1），∠D A C ＝60°.若点 P从点 A出发，沿 A→B→C→D→A…的方向，在菱形的边上以每秒 1 个单位长度的速度移动， 则第 2020 秒时，点 P的坐标为（ ）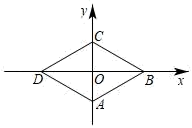
A、（2，0） B、（ ，0） C、（﹣ ，0） D、（0，1 ）二、填空题
-
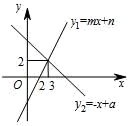
11. 在函数 中，自变量x的取值范围是.12. 一次函数 y1＝mx+n 与 y2＝﹣x+a 的图象如图所示，则 0＜mx+n≤﹣x+a 的解集为.
13. 如图，在△OAB 中，∠AOB＝90°，AO＝3，BO＝4.将△OAB 绕顶点 O 按顺时针方向旋转到△OA1B1 处，此时线段 OB1 与 AB 的交点 D 恰好为线段 AB 的中点， 线段 A1B1 与 OA 交于点 E，则图中阴影部分的面积.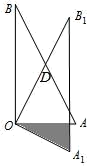
14. 如图，正方形 ABCD 中，AD＝ ，已知点 E 是边 AB 上的一动点（不与A、B 重合）将△ADE 沿 DE 对折，点 A 的对应点为 P，当△APB 是等腰三角形时， 线段 AE= .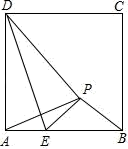
三、解答题
-
15. 先化简，再求值（x﹣ ）÷ ，其中x＝（3cos25°﹣1）0﹣（tan30°）﹣1 ， y＝2cos60°+tan60°.16. 中华文明，源远流长：中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
成绩x/分
频数
频率
50≤x＜60
10
0.05
60≤x＜70
20
0.10
70≤x＜80
30
b
80≤x＜90
a
0.30
90≤x≤100
80
0.40
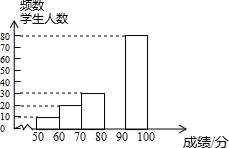
请根据所给信息，解答下列问题：
(1)、a＝ ， b＝；(2)、请补全频数分布直方图；(3)、这次比赛成绩的中位数会落在分数段；(4)、若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？17. 如图所示，在平面直角坐标系中，菱形 ABCD 的边 AD∥x 轴，直线y＝2x+b 与 x 轴交于点 B，与反比例函数 y＝ （k＞0）图象交于点 D 和点 E，OB＝3，OA＝4.
(1)、求反比例函数和一次函数的解析式；(2)、点P为线段 BE 上的一个动点，过点P作x轴的平行线，当△CDE 被这条平行线分成面积相等的两部分时，求点P的坐标.18. 如图， eO 是V ABC 的外接圆，AB 为直径，∠BAC 的平分线交eO 于点 D，过点 D 作 DE⊥AC 分别交 AC、AB 的延长线于点 E、F.
(1)、求证：EF 是eO 的切线；(2)、若 AC=6，CE=3，求弧BD 的长度.（结果保留π）19. 某数学活动小组实地测量湛河两岸互相平行的一段东西走向的河的宽度，在河的北岸边点A处，测得河的南岸边点B处在其南偏东45°方向，然后向北走20米到达点C处，测得点B在点C的南偏东33°方向，求出这段河的宽度.（结果精确到1米，参考数据：sin33°＝0.54，cos33°≈0.84，tan33°＝0.65， ≈1.41）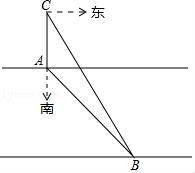
20. “守护碧水蓝天，守护我们的家园”，某市为了改善城市环境，预算 116 万元购进 A、B 两种型号的清扫机，已知 A 型号清扫机的单价比 B 型号清扫 机单价的 多 1.2 万元，若购进 2 台 A 型号清扫机和 3 台 B 型号清扫机花费 54.6 万元.(1)、求 A 型号清扫机和 B 型号清扫机的单价分别为多少万元；(2)、该市通过考察决定先购进两种型号的清扫机共 10 台，且 B 型号的清扫机 数量不能少于 A 型号清扫机的 1.5 倍，该市怎样购买才能花费最少？最少花费 多少万元？21. 问题情境：在综合与实践课上，老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如 图 1，将：矩形纸片 ABCD 沿对角线 AC 剪开，得到△ABC 和△ACD.并且量得 AB ＝4cm，AC＝8cm.
操作发现：
(1)、将图 1 中的△ACD 以点 A 为旋转中心，按逆时针方向旋转∠α，使∠α＝∠BAC，得到如图 2 所示的△AC′D，过点 C 作 AC′的平行线，与 DC'的延长线 交于点 E，则四边形 ACEC′的形状是.(2)、创新小组将图 1 中的△ACD 以点 A 为旋转中心，按逆时针方向旋转，使 B、 A、D 三点在同一条直线上，得到如图 3 所示的△AC′D，连接 CC'，取 CC′的中 点 F，连接 AF 并延长至点 G，使 FG＝AF，连接 CG、C′G，得到四边形 ACGC′， 发现它是正方形，请你证明这个结论.实践探究：
(3)、缜密小组在创新小组发现结论的基础上，进行如下操作：将△ABC 沿着 BD 方向平移，使点 B 与点 A 重合，此时 A 点平移至 A'点，A'C 与 BC′相交于点 H， 如图 4 所示，连接 CC′，试求 tan∠C′CH 的值.22. 如图，已知二次函数 y＝ax2+bx 的图象与 x 轴交于点 O（0，0）和 点 B，抛物线的对称轴是直线 x＝3.点 A 是抛物线在第一象限上的一个动点， 过点 A 作 AC⊥x 轴，垂足为 C.S△AOB＝3S△ABC ， AC2＝OC•BC.
(1)、求该二次函数的解析式；(2)、抛物线的对称轴与 x 轴交于点 M.连接 AM，点 N 是线段 OA 上的一点.当 ∠AMN＝∠AOM 时，求点 N 的坐标；(3)、点 P 是抛物线上的一个动点.点 Q 是 y 轴上的一动点.当以 A，B，P，Q 四个点为顶点的四边形为平行四边形时，直接写出点 P 坐标.