贵州省遵义市2020年数学中考模拟试卷
试卷更新日期:2020-05-12 类型:中考模拟
一、单选题
-
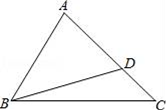
1. 2017年我国大学生毕业人数将达到7490000人,这个数据用科学记数法表示为( )A、 7.49×107 B、74.9×106 C、7.49×106 D、0.749×1072. 如图,直线 与 轴交于点 ,若 时,则 的取值范围是( )
 A、 B、 C、 D、3. "桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客 万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加 ,则可列方程为( )A、 B、 C、 D、4. 甲、乙、丙三地海拔高度分别为30米, 米, 米,那么最高的地方比最低的地方高( )A、20米 B、25米 C、35米 D、55米5. 如图是由几个相同的小正方体搭成的一个几何体,它的左视图是( )
A、 B、 C、 D、3. "桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客 万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加 ,则可列方程为( )A、 B、 C、 D、4. 甲、乙、丙三地海拔高度分别为30米, 米, 米,那么最高的地方比最低的地方高( )A、20米 B、25米 C、35米 D、55米5. 如图是由几个相同的小正方体搭成的一个几何体,它的左视图是( )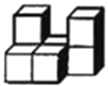 A、
A、 B、
B、 C、
C、 D、
D、 6. 下列计算正确的是( )A、a2+a2=a4 B、2(a﹣b)=2a﹣b C、a3•a2=a5 D、(﹣b2)3=﹣b57. 小明将某圆锥形的冰淇淋纸套沿它的一条母线展开 若不考虑接缝,它是一个半径为12cm,圆心角为 的扇形,则A、圆锥形冰淇淋纸套的底面半径为4cm B、圆锥形冰淇淋纸套的底面半径为6cm C、圆锥形冰淇淋纸套的高为 D、圆锥形冰淇淋纸套的高为8. 某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.
6. 下列计算正确的是( )A、a2+a2=a4 B、2(a﹣b)=2a﹣b C、a3•a2=a5 D、(﹣b2)3=﹣b57. 小明将某圆锥形的冰淇淋纸套沿它的一条母线展开 若不考虑接缝,它是一个半径为12cm,圆心角为 的扇形,则A、圆锥形冰淇淋纸套的底面半径为4cm B、圆锥形冰淇淋纸套的底面半径为6cm C、圆锥形冰淇淋纸套的高为 D、圆锥形冰淇淋纸套的高为8. 某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.成绩
人数(频数)
百分比(频率)
0
5
0.2
10
5
15
0.4
20
5
0.1
根据表中已有的信息,下列结论正确的是( )
A、共有40名同学参加知识竞赛 B、抽到的同学参加知识竞赛的平均成绩为10分 C、已知该校共有800名学生,若都参加竞赛,得0分的估计有100人 D、抽到同学参加知识竞赛成绩的中位数为15分9. 如图,∠1=57°,则∠2的度数为( )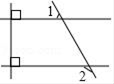 A、120° B、123° C、130° D、147°10. 设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=( )A、﹣5 B、9 C、5 D、711. 在面积为60的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )A、22-11 B、 C、 或 D、 或12. 如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(﹣1,0),A点的横坐标是2,AB=3BC,双曲线y= (m>0)经过A点,双曲线y=﹣ 经过C点,则m的值为( )
A、120° B、123° C、130° D、147°10. 设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=( )A、﹣5 B、9 C、5 D、711. 在面积为60的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=10,BC=12,则CE+CF的值为( )A、22-11 B、 C、 或 D、 或12. 如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(﹣1,0),A点的横坐标是2,AB=3BC,双曲线y= (m>0)经过A点,双曲线y=﹣ 经过C点,则m的值为( )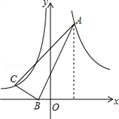 A、12 B、9 C、6 D、3
A、12 B、9 C、6 D、3二、填空题
-
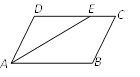
13. 计算 = , (﹣ )2= , 3 ﹣ =.14. 如图,在平行四边形ABCD中,∠BAD的平分线AE交边CD于E, AB=5cm,EC=2cm则BC=cm.
 15. 如图,在Rt△ABC中,∠ACB = 90°, ,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE = .
15. 如图,在Rt△ABC中,∠ACB = 90°, ,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE = .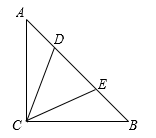
三、解答题
-
16. 计算: .17. 先化简,再求值:( + )÷ ,其中x= .18. 某校美术组要购买铅笔和橡皮,按照商店规定,若同时购买60支铅笔和30块橡皮,则需按零售价购买,共需支付30元;若同时购买90支铅笔和60块橡皮,则可按批发价购买,共需支付40.5元.已知每支铅笔的批发价比零售价低0.05元,每块橡皮的批发价比零售价低0.10元.求每支铅笔和每块橡皮的批发价各是多少元?19. 某中学开展“一起阅读,共同成长”课外读书周活动,活动后期随机调查了八年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:
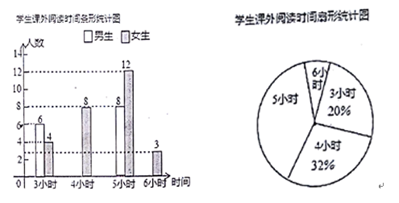 (1)、本次调查的学生总数为人,在扇形统计图中,课外阅读时间为5小时的扇形圆心角度数是;(2)、请你补全条形统计图;(3)、若全校八年级共有学生 人,估计八年级一周课外阅读时间至少为 小时的学生有多少人?20. 已知:如图,为了躲避台风,一轮船一直由西向东航行,上午 点,在 处测得小岛 的方向是北偏东 ,以每小时 海里的速度继续向东航行,中午 点到达 处,并测得小岛 的方向是北偏东 ,若小岛周围 海里内有暗礁,问该轮船是否能一直向东航行?
(1)、本次调查的学生总数为人,在扇形统计图中,课外阅读时间为5小时的扇形圆心角度数是;(2)、请你补全条形统计图;(3)、若全校八年级共有学生 人,估计八年级一周课外阅读时间至少为 小时的学生有多少人?20. 已知:如图,为了躲避台风,一轮船一直由西向东航行,上午 点,在 处测得小岛 的方向是北偏东 ,以每小时 海里的速度继续向东航行,中午 点到达 处,并测得小岛 的方向是北偏东 ,若小岛周围 海里内有暗礁,问该轮船是否能一直向东航行?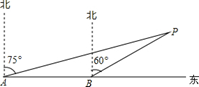 21. 在以点O为原点的平面直角坐标系中,边长为1的正方形OABC的两顶点A,C分别在y轴, 轴的正半轴上,现将正方形OABC绕点О顺时针旋转,当点A第一次落在直线 上时,停止转动,旋转过程中,AB边交直线 于点M,BC边交轴于点N.
21. 在以点O为原点的平面直角坐标系中,边长为1的正方形OABC的两顶点A,C分别在y轴, 轴的正半轴上,现将正方形OABC绕点О顺时针旋转,当点A第一次落在直线 上时,停止转动,旋转过程中,AB边交直线 于点M,BC边交轴于点N.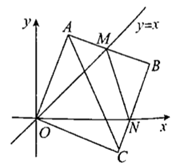 (1)、旋转停止时正方形旋转的度数是.(2)、在旋转过程中,当MN和AC平行时,
(1)、旋转停止时正方形旋转的度数是.(2)、在旋转过程中,当MN和AC平行时,① 与 是否全等?此时正方形OABC旋转的度数是多少?
②直接写出 的周长的值,并判断这个值在正方形OABC的旋转过程中是否发生变化.