贵州省铜仁市2020年数学中考模拟试卷

试卷更新日期：2020-05-12 类型：中考模拟

进入出卷网下载

一、单选题

1. －2的相反数是（）

A、2 B、－2 C、±2 D、－ $\frac{1}{2}$

查看试题解析
2. 下列方程中,没有实数根的方程是（）

A、 $x^{2} + 2 x - 1 = 0$ B、 $x^{2} + 2 x + 1 = 0$ C、 $x^{2} - x + 2 = 0$ D、 $x^{2} - x - 2 = 0$

查看试题解析
3. 港珠澳大桥总投资1100亿，那么1100用科学记数法表示为（）

A、 $1.1 \times 10^{3}$ B、 $1.1 \times 10^{4}$ C、 $11 \times 10^{2}$ D、 $0.11 \times 10^{4}$

查看试题解析
4. 在2017年的初中数学竞赛中，我校有5位同学获奖，他们的成绩分别是88，86，91，88，92.则由这组数据得到的以下结论，错误的是（）

A、极差为6 B、平均数为89 C、众数为88 D、中位数为91

查看试题解析
5. 一个多边形切去一个角后得到的另一个多边形的内角和为 $900 °$ ，那么原多边形的边数为（）

A、6或7或8 B、6或7 C、7或8 D、7

查看试题解析
6. 如图，一条公路的转弯处是一段圆弧，点 $O$ 是这段弧所在圆的圆心， $A B = 40 m$ ，点 $C$ 是 $\overset{⌢}{A B}$ 的中点，点D是AB的中点，且 $C D = 10 m$ ，则这段弯路所在圆的半径为（）

A、 $25 m$ B、 $24 m$ C、 $30 m$ D、 $60 m$

查看试题解析
7. 如图，直线 $A B / / C D$ ，AG平分 $∠ B A E$ ， $∠ E F C = 40^{\circ}$ ，则 $∠ G A F$ 的度数为（）

A、 $110^{\circ}$ B、 $115^{\circ}$ C、 $125^{\circ}$ D、 $130^{\circ}$

查看试题解析
8. 如图：△ABC是等边三角形，AE＝CD，AD，BE相交于点P，BQ⊥AD于Q，PQ＝4，PE＝1，则AD的长是（）

A、9 B、8 C、7 D、6

查看试题解析
9. 如图，在平行四边形ABCD中，E，F分别是边AD，BC的中点，AC分别交BE，DF于G，H，试判断下列结论：①△ABE≌△CDF；②AG＝GH＝HC；③2EG＝BG；④S_△_ABG：S_四边形_GHDE＝2：3，其中正确的结论是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图1，在 $R t △ A B C$ 中， $∠ A = 90^{\circ}$ ， $B C = 10 c m$ ，点P、点Q同时从点B出发，点P以 $2 c m / s$ 的速度沿 $B \to A \to C$ 运动，终点为C，点Q以 $1 c m / s$ 的速度沿 $B \to C$ 运动，当点P到达终点时两个点同时停止运动，设点P，Q出发t秒时， $△ B P Q$ 的面积为 $y c m^{2}$ ，已知y与t的函数关系的图象如图 $2 ($ 曲线OM和MN均为抛物线的一部分 $)$ ，给出以下结论： $① A C = 6 c m$ ； $②$ 曲线MN的解析式为 $y = - \frac{4}{5} t^{2} + \frac{28}{5} t (4 \leq t \leq 7)$ ； $③$ 线段PQ的长度的最大值为 $\frac{6}{5} \sqrt{10}$ ； $④$ 若 $△ P Q C$ 与 $△ A B C$ 相似，则 $t = \frac{40}{7}$ 秒 $.$ 其中正确的是 $($ ）

A、 $① ② ④$ B、 $② ③ ④$ C、 $① ③ ④$ D、 $① ② ③$

查看试题解析

二、填空题

11. 在实数范围内分解因式： $a^{4} - 9$ =.

查看试题解析
12. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好是9.4环，方差分别是 $S_{甲}^{2} = 0 ． 90$ ， $S_{乙}^{2} = 1.22$ ， $S_{丙}^{2} = 0.43$ ， $S_{丁}^{2} = 1.68$ ，在本次射击测试中，成绩最稳定的是.

查看试题解析
13. 分式方程 $\frac{3 - 2 x}{x - 2}$ + $\frac{2}{2 - x}$ =1的解为.

查看试题解析
14. 某企业退休职工李师傅2013年月退休金为1500元，2015年达到2160元.设李师傅的月退休金从2013年到2015年年平均增长率为x，可列方程为.

查看试题解析
15. 已知关于x的不等式组 ${\begin{array}{l} 5 - 2 x \geq - 1 \\ x - a > 0 \end{array}$ 有3个整数解，则a的取值范围是.

查看试题解析
16. 如图，ABCD是⊙O的内接四边形，AB是⊙O的直径，过点D的切线交BA的延长线于点E，若∠ADE＝25°，则∠C＝度.

查看试题解析
17. 如图，在Rt△ABC中，∠BAC=90°，AB=1，tanC= $\frac{2}{3}$ ，以点A为圆心，AB长为半径作弧交AC于D，分别以B、D为圆心，以大于 $\frac{1}{2}$ BD长为半径作弧，两弧交于点E，射线AE与BC于F，过点F作FG⊥AC于G，则FG的长为．

查看试题解析
18. 正整数按如图的规律排列，请写出第10行，第10列的数字.

查看试题解析

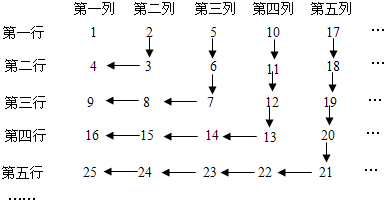
三、解答题

19. 计算： $5^{0} - (- 2) + \sqrt{8} \times \sqrt{2}$

查看试题解析

20. 某校为了解学生体质情况，从各年级学生中随机抽取部分学生进行体能测试.

每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现，优秀漏统计4人，良好漏统计6人，于是及时更正，从而形成如下图表.请按正确数据解答下列各题：

体能等级	调整前人数	调整后人数
优秀
良好
及格
不及格
合计

(1)、填写统计表.

(2)、根据调整后数据，补全条形统计图.

(3)、若该校共有学生1500人，请你估算出该校体能测试等级为“优秀”的人数.

查看试题解析

21. △ABC中，AB＝AC，∠BAC＝120°，点D、F分别为AB、AC中点，ED⊥AB，GF⊥AC，若BC＝15cm，求EG的长.

查看试题解析
22. 如图，在四边形ABCD中，AD∥BC，点O是对角线AC的中点，过点O作AC的垂线，分别交AD、BC于点E、F，连结AF、CE.

(1)、求证：△AOE≌△COF.

(2)、试判断四边形AFCE的形状，并证明.

查看试题解析
23. 已知：如图，反比例函数 $y_{1} = \frac{k}{x}$ 的图象与一次函数 $y_{2} = x + b$ 的图象交于点 $A (1 ， 4)$ ，点 $B (- 4 ， n)$ .

(1)、求一次函数和反比例函数的解析式；

(2)、求 $△ O A B$ 的面积；

(3)、根据图象，试比较 $y_{1}$ ， $y_{2}$ 的大小.

查看试题解析
24. 如图1，DE是⊙O的直径，点A、C是直径DE上方半圆上的两点，且AO⊥CO.连接AE，CD相交于点F，点B是直径DE下方半圆上的任意一点，连接AB交CD于点G，连接CB交AE于点H.

(1)、∠ABC＝；

(2)、证明：△CFH∽△CBG；

(3)、若弧DB为半圆的三分之一，把∠AOC绕着点O旋转，使点C、O、B在一直线上时，如图2，求 $\frac{F H}{B G}$ 的值.

查看试题解析
25. 如图在平面直角坐标系中顶点为点M的抛物线是由抛物线 $y = x^{2} - 3$ 向右平移1个单位得到的，它与y轴负半轴交于点A，点B在抛物线上，且横坐标为3.

(1)、写出以M为顶点的抛物线解析式.

(2)、连接AB，AM，BM，求 $tan ∠ A B M$ ；

(3)、点P是顶点为M的抛物线上一点，且位于对称轴的右侧，设PO与x正半轴的夹角为 $α$ ，当 $α = ∠ A B M$ 时，求点P坐标.

查看试题解析