广西贵港市2020年初中学业水平考试数学模拟试卷
试卷更新日期:2020-05-12 类型:中考模拟
一、单选题
-
1. 计算 的正确结果是( )A、 B、2 C、8 D、-22. 如图所示,该几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 长江三峡工程电站的总装机容量用科学记数法表示为1.82×107千瓦,把它写成原数是( )A、182000千瓦 B、182000000千瓦 C、18200000千瓦 D、1820000千瓦4. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如果 在第三象限,那么点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若 是一元二次方程 的两根 ,则 =( )A、 B、2 C、3 D、58. 下列命题中,真命题是( )A、若 ,则 B、当 是一切实数时, C、四边形的内角和与外角和相等 D、垂直于同一直线地两条直线平行9. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC的度数是( )
3. 长江三峡工程电站的总装机容量用科学记数法表示为1.82×107千瓦,把它写成原数是( )A、182000千瓦 B、182000000千瓦 C、18200000千瓦 D、1820000千瓦4. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 如果 在第三象限,那么点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若 是一元二次方程 的两根 ,则 =( )A、 B、2 C、3 D、58. 下列命题中,真命题是( )A、若 ,则 B、当 是一切实数时, C、四边形的内角和与外角和相等 D、垂直于同一直线地两条直线平行9. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC的度数是( ) A、35° B、55° C、65° D、70°10. 如图,在 中, , 分别是 的边 , 上的中线,则 ( )
A、35° B、55° C、65° D、70°10. 如图,在 中, , 分别是 的边 , 上的中线,则 ( ) A、 B、 C、 D、11. 如图,在等腰直角三角形ABC中,AB=AC=2,∠BAC=90°,点D是AC的中点,点P是BC边上的动点,连接PA、PD.则PA+PD的最小值为( )
A、 B、 C、 D、11. 如图,在等腰直角三角形ABC中,AB=AC=2,∠BAC=90°,点D是AC的中点,点P是BC边上的动点,连接PA、PD.则PA+PD的最小值为( ) A、 B、 C、 D、312. 如图,四边形 是边长为1的正方形, 为 所在直线上的两点,若 ,则下列结论正确的是( )
A、 B、 C、 D、312. 如图,四边形 是边长为1的正方形, 为 所在直线上的两点,若 ,则下列结论正确的是( ) A、 B、 C、 D、四边形 的面积为
A、 B、 C、 D、四边形 的面积为二、填空题
-
13. 分解因式:3y2﹣12=.14. 如图,直线 , 被直线 所截,若 , , ,则 °.
 15. 有9张相同的片,每张片上分别写有1-9的自然数,从中任取张卡片,则抽到卡片上的数字是3的整数倍的概率为.16. 如图,在扇形 中, ,点 为 的中点, 交弧 于点 ,以点 为圆心, 的长为半径作弧 交 于点 ,若 ,则阴影部分的面积为.
15. 有9张相同的片,每张片上分别写有1-9的自然数,从中任取张卡片,则抽到卡片上的数字是3的整数倍的概率为.16. 如图,在扇形 中, ,点 为 的中点, 交弧 于点 ,以点 为圆心, 的长为半径作弧 交 于点 ,若 ,则阴影部分的面积为. 17. 如图,已知抛物线 ,直线 ,当 任取一值时, 对应的函数值分别 为 ,若 ,取 中的较小值记为 ;若 ,记 ,例如:当 时, ,此时 ,下列判断:
17. 如图,已知抛物线 ,直线 ,当 任取一值时, 对应的函数值分别 为 ,若 ,取 中的较小值记为 ;若 ,记 ,例如:当 时, ,此时 ,下列判断:①当 时, ;
②当 时, 值越大, 值越小;
③使得 大于2的 值不存在;
④使得 的 值是 或 .

其中正确的是.
三、解答题
-
18.(1)、计算:3﹣2﹣2cos30°+(3﹣π)0﹣| ﹣2|;(2)、解不等式组 ,并把解集在如图所示的数轴上表示出来.
 19. 如图,已知 ,请用尺规在 中找一点 ,使得点 到 三边的距离相等.(保留作图痕迹,不写作法)
19. 如图,已知 ,请用尺规在 中找一点 ,使得点 到 三边的距离相等.(保留作图痕迹,不写作法) 20. 如图,一次函数 的图象与反比例函数 的图象交于 两点,与 轴交于点 ,与 轴于点 ,点 的坐标为 ,点 的坐标为 .
20. 如图,一次函数 的图象与反比例函数 的图象交于 两点,与 轴交于点 ,与 轴于点 ,点 的坐标为 ,点 的坐标为 . (1)、求反比例函数与一次函数的解析式;(2)、求 的面积.21. 某学校在暑假期间开展“心怀感恩、孝敬父母”的实践活动,倡导学生在假期中帮助父母干家务,开学以后,校学生会随机抽取了部分学生,就暑假“平均每天帮助父母干家务所用时长”进行了调查,以下是根据相关数据绘制的统计图.
(1)、求反比例函数与一次函数的解析式;(2)、求 的面积.21. 某学校在暑假期间开展“心怀感恩、孝敬父母”的实践活动,倡导学生在假期中帮助父母干家务,开学以后,校学生会随机抽取了部分学生,就暑假“平均每天帮助父母干家务所用时长”进行了调查,以下是根据相关数据绘制的统计图.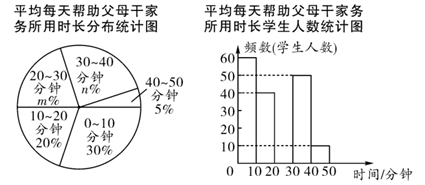
根据上述信息,回答下列问题:
(1)、在本次随机抽取的样本中,调查的学生人数为.(2)、补全频数分布直方图;(3)、如果该校共有学生1000人,表你估计“平均每天帮助父母干家务所用时长不少于30分钟”的学生有多少人.22. 某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示进价 元 千克
售价 元 千克
A种水果
5
8
B种水果
9
13
(1)、若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?(2)、在(1)的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价 出售,那么售完后共获利多少元?23. 如图,M,N是以AB为直径的⊙O上的点,且 = ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F. (1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.24. 如图,在平面直角坐标系中, ,点 的坐标为 ,抛物线 经过 两点.
(1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.24. 如图,在平面直角坐标系中, ,点 的坐标为 ,抛物线 经过 两点. (1)、求抛物线的解析式;(2)、点 是直线 上方抛物线上的一点,过点 作 轴于点 ,交线段 于点 ,使 .
(1)、求抛物线的解析式;(2)、点 是直线 上方抛物线上的一点,过点 作 轴于点 ,交线段 于点 ,使 .①求点 的坐标和 的面积;
②在直线 上是否存在点 ,使 为直角三角形?若存在,直接写出符合条件的所有点 的坐标;若不存在,请说明理由.
25. 已知: 是 的高,且 .(1)、如图1,求证: ;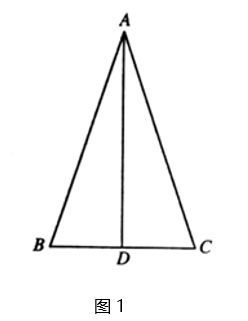 (2)、如图2,点E在AD上,连接 ,将 沿 折叠得到 , 与 相交于点 ,若BE=BC,求 的大小;
(2)、如图2,点E在AD上,连接 ,将 沿 折叠得到 , 与 相交于点 ,若BE=BC,求 的大小;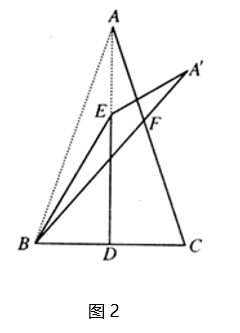 (3)、如图3,在(2)的条件下,连接 ,过点 作 ,交 的延长线于点 ,若 , ,求线段 的长.
(3)、如图3,在(2)的条件下,连接 ,过点 作 ,交 的延长线于点 ,若 , ,求线段 的长.