2015年江苏省徐州市中考数学真题试卷
试卷更新日期：2016-04-25 类型：中考真卷
一、单选题（本大题共8小题，每小题3分，共24分）
-
1. ﹣2的倒数是（ ）A、2 B、-2 C、 D、-2. 下列四个几何体中，主视图为圆的是（ ）
A、
B、
C、
D、
3. 下列运算正确的是（ ）A、3a2﹣2a2=1 B、（a2）3=a5 C、a2•a4=a6 D、（3a）2=6a24. 使有意义的x的取值范围是（ ）
A、x≠1 B、x≥1 C、x＞1 D、x≥05. 一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是（ ）A、至少有1个球是黑球 B、至少有1个球是白球 C、至少有2个球是黑球 D、至少有2个球是白球6. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）A、直角三角形 B、正三角形 C、平行四边形 D、正六边形7.如图，菱形中，对角线AC、BD交于点O，E为AD边中点，菱形ABCD的周长为28，则OE的长等于（ ）
A、3.5 B、4 C、7 D、148.若函数y=kx﹣b的图象如图所示，则关于x的不等式k（x﹣3）﹣b＞0的解集为（ ）
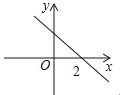A、x＜2 B、x＞2 C、x＜5 D、x＞5二、填空题（本大题共10小题，每小题3分，共30分）
-
9. 4是 的算术平方根．10. 杨絮纤维的直径约为0.000 010 5m，该直径用科学记数法表示为 .
11. 小丽近6个月的手机话费（单位：元）分别为：18，24，37，28，24，26，这组数据的中位数是 元．12. 若正多边形的一个内角等于140°，则这个正多边形的边数是 .
13. 已知关于x的一元二次方程x2﹣2x﹣k=0有两个相等的实数根，则k值为 .
14.如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA= .
15.如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC．若∠CAB=22.5°，CD=8cm，则⊙O的半径为 cm．
16.如图，在△ABC中，∠C=31°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A= .
17.如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形，再以对角线AE为边作第三个正方形AEGH，如此下去，第n个正方形的边长为 .
18. 用一个圆心角为90°，半径为4的扇形围成一个圆锥的侧面，该圆锥底面圆的半径三、解答题（本大题共10小题，共86分）
-
19.
计算：
（1）|﹣4|﹣20150+（）﹣1﹣（）2
（2）（1+）÷ ．
20. （1）解方程：x2﹣2x﹣3=0；（2）解不等式组：
21.小明参加某网店的“翻牌抽奖”活动，如图，4张牌分别对应价值5，10，15，20（单位：元）的4件奖品．
(1)、如果随机翻1张牌，那么抽中20元奖品的概率为(2)、如果随机翻2张牌，且第一次翻过的牌不再参加下次翻牌，则所获奖品总值不低于30元的概率为多少？22.某校分别于2012年、2014年随机调查相同数量的学生，对数学课开展小组合作学习的情况进行调查（开展情况分为较少、有时、常常、总是四种），绘制成部分统计图如下．请根据图中信息，解答下列问题：
(1)、a=%，b=%，“总是”对应阴影的圆心角为(2)、请你补全条形统计图(3)、若该校2014年共有1200名学生，请你统计其中认为数学课“总是”开展小组合作学习的学生有多少名？(4)、相比2012年，2014年数学课开展小组合作学习的情况有何变化？23.如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．
(1)、求证：四边形BFCE是平行四边形(2)、若AD=10，DC=3，∠EBD=60°，则BE= 时，四边形BFCE是菱形24. 某超市为促销，决定对A，B两种商品进行打折出售．打折前，买6件A商品和3件B商品需要54元，买3件A商品和4件B商品需要32元；打折后，买50件A商品和40件B商品仅需364元，这比打折前少花多少钱？25.如图，平面直角坐标系中，将含30°的三角尺的直角顶点C落在第二象限．其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm。
(1)、（1）若OB=6cm．①求点C的坐标；②若点A向右滑动的距离与点B向上滑动的距离相等，求滑动的距离
(2)、点C与点O的距离的最大值= cm．26.如图，在矩形 OABC中，OA=3，OC=5，分别以 OA、OC所在直线为x 轴、y 轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y=（k＞0）的图象经过点D且与边BA交于点E，连接DE．
(1)、连接OE，若△EOA的面积为2，则k=(2)、连接CA，DE与CA是否平行？请说明理由：
(3)、是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由：
27.为加强公民的节水意识，合理利用水资源．某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于1：1.5：2．如图折线表示实行阶梯水价后每月水费y（元）与用水量xm3之间的函数关系．其中线段AB表示第二级阶梯时y与x之间的函数关系。
(1)、写出点B的实际意义(2)、求线段AB所在直线的表达式(3)、某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？28.如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD⊥x轴于点D，交线段OB于点E，已知CD=8，抛物线经过O、E、A三点．
(1)、∠OBA=(2)、求抛物线的函数表达式(3)、若P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形面积记作S，则S取何值时，相应的点P有且只有3个？