2015年江苏省宿迁市中考数学真题试卷
试卷更新日期：2016-04-25 类型：中考真卷
一、单选题（本大题共8小题，每小题3分，共24分）
-
1. -的倒数是（ ）A、-2 B、2 C、- D、2. 若等腰三角形中有两边长分别为2和5，则这个三角形的周长为（ ）A、9 B、12 C、7或9 D、9或123. 计算（﹣a3）2的结果是（ ）A、﹣a5 B、a5 C、﹣a6 D、a64.
如图所示，直线a，b被直线c所截，∠1与∠2是（ ）
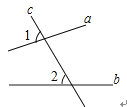A、同位角 B、内错角 C、同旁内角 D、邻补角5. 函数y= ， 自变量x的取值范围是（ ）A、x＞2 B、x＜2 C、x≥2 D、x≤26. 已知一个多边形的内角和等于它的外角和，则这个多边形的边数为（ ）A、3 B、4 C、5 D、67. 在平面直角坐标系中，点A，B的坐标分别为（﹣3，0），（3，0），点P在反比例函数y=的图象上，若△PAB为直角三角形，则满足条件的点P的个数为（ ）A、2个 B、4个 C、5个 D、6个二、填空题（本大题共8小题，每小题3分，共24分）
-
8. 某市今年参加中考的学生大约为45000人，将数45000用科学记数法可以表示为 .9. 关于x的不等式组的解集为1＜x＜3，则a的值为 .
10. 因式分解：x3﹣4x= .
11. 方程﹣=0的解是 .
12.如图，四边形ABCD是⊙O的内接四边形，若∠C=130°，则∠BOD=
13.如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为
14.如图，在平面直角坐标系中，点P的坐标为（0，4），直线y=x﹣3与x轴、y轴分别交于点A，B，点M是直线AB上的一个动点，则PM长的最小值为
15. 当x=m或x=n（m≠n）时，代数式x2﹣2x+3的值相等，则x=m+n时，代数式x2﹣2x+3的值为三、解答题（本大题共10小题，共72分，解答时应写出必要的文字说明、证明过程或演算步骤）
-
16. 计算：cos60°﹣2﹣1+﹣（π﹣3）0 ．17. （1）解方程：x2+2x=3；
（2）解方程组：
18.某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：kg）分成五组（A：39.5～46.5；B：46.5～53.5；C：53.5～60.5；D：60.5～67.5；E：67.5～74.5），并依据统计数据绘制了如下两幅尚不完整的统计图．
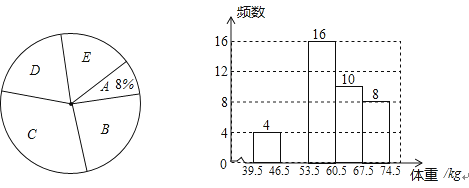
解答下列问题：
(1)、这次抽样调查的样本容量是 ， 并补全频数分布直方图(2)、C组学生的频率为 ，在扇形统计图中D组的圆心角是 度(3)、请你估计该校初三年级体重超过60kg的学生大约有多少名？19. 一只不透明的袋子中装有1个白球、1个蓝球和2个红球，这些球除颜色外都相同．(1)、从袋中随机摸出1个球，摸出红球的概率为(2)、从袋中随机摸出1个球（不放回）后，再从袋中余下的3个球中随机摸出1个球．求两次摸到的球颜色不相同的概率．20.如图，已知AB=AC=AD，且AD∥BC，求证：∠C=2∠D．
21.如图，观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上，从点A处测得楼顶端B的仰角为22°，此时点E恰好在AB上，从点D处测得楼顶端B的仰角为38.5°．已知旗杆DE的高度为12米，试求楼房CB的高度．（参考数据：sin22°≈0.37，cos22°≈0.93，tan22°≈0.40，sin38.5°≈0.62，cos38.5°≈0.78，tan38.5°≈0.80）
22.如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F
(1)、求证：四边形BDFC是平行四边形。
(2)、若△BCD是等腰三角形，求四边形BDFC的面积．23.如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数y=（x＞0）的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．
(1)、求k的值。
(2)、求△BMN面积的最大值。
(3)、若MA⊥AB，求t的值。
24.已知：⊙O上两个定点A，B和两个动点C，D，AC与BD交于点E．
(1)、如图1，求证：EA•EC=EB•ED(2)、如图2，若
， AD是⊙O的直径，求证：AD•AC=2BD•BC(3)、如图3，若AC⊥BD，点O到AD的距离为2，求BC的长25.如图，在平面直角坐标系中，正方形ABCD和正方形DEFG的边长分别为2a，2b，点A，D，G在y轴上，坐标原点O为AD的中点，抛物线y=mx2过C，F两点，连接FD并延长交抛物线于点M．
(1)、若a=1，求m和b的值。
(2)、求的值。
(3)、判断以FM为直径的圆与AB所在直线的位置关系，并说明理由．