2015年江苏省无锡市中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣3的倒数是（　　）

A、3 B、±3 C、 $\frac{1}{3}$ D、- $\frac{1}{3}$

查看试题解析
2. 函数y= $\sqrt{x - 4}$ 中自变量x的取值范围是（　　）

A、x＞4 B、x≥4 C、x≤4 D、x≠4

查看试题解析
3. 今年江苏省参加高考的人数约为393000人，这个数据用科学记数法可表示为（　　）

A、393×10³ B、3.93×10³ C、3.93×10⁵ D、3.93×10⁶

查看试题解析
4. 方程2x﹣1=3x+2的解为（　　）

A、x=1 B、x=-1 C、x=3 D、x=-3

查看试题解析
5. 若点A（3，﹣4）、B（﹣2，m）在同一个反比例函数的图象上，则m的值为（　　）

A、6 B、-6 C、12 D、-12

查看试题解析
6. 下列图形中，是轴对称图形但不是中心对称图形的是（　　）

A、等边三角形 B、平行四边形 C、矩形 D、圆

查看试题解析
7. tan45°的值为（　　）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{2}}{2}$ D、 $\sqrt{2}$

查看试题解析
8. 八边形的内角和为（　　）

A、180° B、360° C、1080° D、1440°

查看试题解析
9.
如图的正方体盒子的外表面上画有3条粗黑线，将这个正方体盒子的表面展开（外表面朝上），展开图可能是（　　）

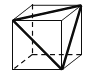A、 B、 C、 D、

查看试题解析
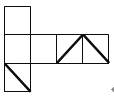10.
如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为（　　）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{2}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析

二、填空题

11. 分解因式：8﹣2x²= .

查看试题解析
12. 化简 $\frac{2 x + 6}{x^{2} - 9}$ 得 .

查看试题解析
13. 一次函数y=2x﹣6的图象与x轴的交点坐标为 .

查看试题解析
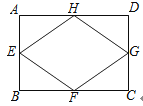
14.
如图，已知矩形ABCD的对角线长为8cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长等于 cm．

查看试题解析
15. 命题“全等三角形的面积相等”的逆命题是命题．（填入“真”或“假”）

查看试题解析
16. 某种蔬菜按品质分成三个等级销售，销售情况如表：
等级
单价（元/千克）
销售量（千克）
一等
5.0
20
二等
4.5
40
三等
4.0
40
则售出蔬菜的平均单价为　元/千克．

查看试题解析
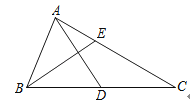
17.
已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD=BE=6，则AC的长等于 .

查看试题解析
18. 某商场在“五一”期间举行促销活动，根据顾客按商品标价一次性购物总额，规定相应的优惠方法：①如果不超过500元，则不予优惠；②如果超过500元，但不超过800元，则按购物总额给予8折优惠；③如果超过800元，则其中800元给予8折优惠，超过800元的部分给予6折优惠．促销期间，小红和她母亲分别看中一件商品，若各自单独付款，则应分别付款480元和520元；若合并付款，则她们总共只需付款元．

查看试题解析

三、综合题

19. 计算：
（1）（﹣5）⁰﹣（ $\sqrt{3}$ ）²+|﹣3|；（2）（x+1）²﹣2（x﹣2）．

查看试题解析
20.
（1）解不等式：2（x﹣3）﹣2≤0
（2）解方程组：

查看试题解析
21.
已知：如图，AB∥CD，E是AB的中点，CE=DE．

(1)、求证：∠AEC=∠BED

(2)、求证：AC=BD

查看试题解析
22.
已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC=6cm，AC=8cm，∠ABD=45°．

(1)、求BD的长

(2)、求图中阴影部分的面积

查看试题解析
23.
某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查，其中有这样一个问题：
老师在课堂上放手让学生提问和表达，　
A．从不 B．很少 C．有时 D．常常 E．总是
答题的学生在这五个选项中只能选择一项．如图是根据学生对该问题的答卷情况绘制的两幅不完整的统计图．
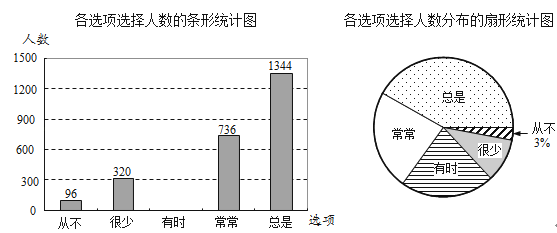
根据以上信息，解答下列问题：

(1)、该区共有名初二年级的学生参加了本次问卷调查

(2)、请把这幅条形统计图补充完整

(3)、在扇形统计图中，“总是”所占的百分比为

查看试题解析
24. （1）甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人．

(1)、求第二次传球后球回到甲手里的概率．（请用“画树状图”或“列表”等方式给出分析过程）

(2)、如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是

查看试题解析
25. 某工厂以80元/箱的价格购进60箱原材料，准备由甲、乙两车间全部用于生产A产品．甲车间用每箱原材料可生产出A产品12千克，需耗水4吨；乙车间通过节能改造，用每箱原材料可生产出的A产品比甲车间少2千克，但耗水量是甲车间的一半．已知A产品售价为30元/千克，水价为5元/吨．如果要求这两车间生产这批产品的总耗水量不得超过200吨，那么该厂如何分配两车间的生产任务，才能使这次生产所能获取的利润w最大？最大利润是多少？（注：利润=产品总售价﹣购买原材料成本﹣水费）

查看试题解析
26. 已知：平面直角坐标系中，四边形OABC的顶点分别为O（0，0）、A（5，0）、B（m，2）、C（m﹣5，2）．

(1)、问：是否存在这样的m，使得在边BC上总存在点P，使∠OPA=90°？若存在，求出m的取值范围；若不存在，请说明理由．

(2)、当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值．

查看试题解析
27.
一次函数y= $\frac{3}{4}$ x的图象如图所示，它与二次函数y=ax²﹣4ax+c的图象交于A、B两点（其中点A在点B的左侧），与这个二次函数图象的对称轴交于点C．

(1)、求点C的坐标

(2)、设二次函数图象的顶点为D．
①若点D与点C关于x轴对称，且△ACD的面积等于3，求此二次函数的关系式；
②若CD=AC，且△ACD的面积等于10，求此二次函数的关系式．

查看试题解析
28.
如图，C为∠AOB的边OA上一点，OC=6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．

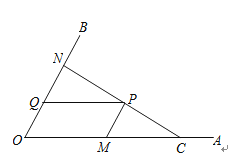(1)、若∠AOB=60°，OM=4，OQ=1，求证：CN⊥OB

(2)、当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
①问： $\frac{1}{O M}$ ﹣ $\frac{1}{O N}$ 的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
②设菱形OMPQ的面积为S₁ ， △NOC的面积为S₂ ，求 $\frac{S_{1}}{S_{2}}$ 的取值范围．

查看试题解析

等级	单价（元/千克）	销售量（千克）
一等	5.0	20
二等	4.5	40
三等	4.0	40