2015年江苏省苏州市中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、选择题：本大题共共10小题，每小题3分，满分30分

1. 2的相反数是（　　）

A、2 B、 $\frac{1}{2}$ C、-2 D、- $\frac{1}{2}$

查看试题解析
2. 有一组数据：3，5，5，6，7，这组数据的众数为（　　）

A、3 B、5 C、6 D、7

查看试题解析
3. 月球的半径约为1738000m，1738000这个数用科学记数法可表示为（　　）

A、1.738×10⁶ B、1.738×10⁷ C、0.1738×10⁷ D、17.38×10⁵

查看试题解析
4. 若m= $\frac{\sqrt{2}}{2}$ ×（﹣2），则有（　　）

A、0＜m＜1 B、﹣1＜m＜0 C、﹣2＜m＜﹣1 D、﹣3＜m＜﹣2

查看试题解析
5. 小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：
通话时间x/min
0＜x≤5
5＜x≤10
10＜x≤15
15＜x≤20
频数（通话次数）
20
16
9
5
则通话时间不超过15min的频率为（　　）

A、0.1 B、0.4 C、0.5 D、0.9

查看试题解析
6. 若点A（a，b）在反比例函数y= $\frac{2}{x}$ 的图象上，则代数式ab﹣4的值为（　　）

A、0 B、-2 C、2 D、-6

查看试题解析
7.
如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为（　　）

A、35° B、45° C、55° D、60°

查看试题解析
8. 若二次函数y=x²+bx的图象的对称轴是经过点（2，0）且平行于y轴的直线，则关于x的方程x²+bx=5的解为（　　）

A、x₁=0，x₂=4 B、x₁=1，x₂=5 C、x₁=1，x₂=﹣5 D、x₁=﹣1，x₂=5

查看试题解析
9.
如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD．若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为（　　）

A、 $\frac{4 π}{3} - \sqrt{3}$ B、 $\frac{4 π}{3} - 2 \sqrt{3}$ C、 $π - \sqrt{3}$ D、 $\frac{2 π}{3} - \sqrt{3}$

查看试题解析
10.
如图，在一笔直的海岸线l上有A、B两个观测站，AB=2km、从A测得船C在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则船C离海岸线l的距离（即CD的长）为（　　）

A、4km B、（2+ $\sqrt{2}$ ）km C、2 $\sqrt{2}$ km D、（4﹣ $\sqrt{2}$ ）km

查看试题解析

二、填空题（本大题共8小题，每小题3分，满分24分，把答案直接填在答题卡相应位置上）

11. 计算：a•a²=

查看试题解析
12.
如图，直线a∥b，∠1=125°，则∠2的度数为

查看试题解析
13.
某学校“你最喜爱的球类运动”调查中，随机调查了若干名学生（每个学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为　名．

查看试题解析
14. 分解因式：a²﹣4b²=

查看试题解析
15.
如图，转盘中8个扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 .

查看试题解析
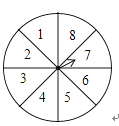16. 若a﹣2b=3，则9﹣2a+4b的值为

查看试题解析
17.
如图，在△ABC中，CD是高，CE是中线，CE=CB，点A、D关于点F对称，过点F作FG∥CD，交AC边于点G，连接GE．AC=18，BC=12，则△CEG的周长为

查看试题解析
18.
如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF=4．设AB=x，AD=y，则x²+（y﹣4）²的值为 .

查看试题解析

三、解答题

19. 计算： $\sqrt{9}$ +|﹣5|﹣（2﹣ $\sqrt{3}$ ）⁰ ．

查看试题解析
20. 解不等式组： $\{\begin{matrix} x + 1 \geq 2 \\ 3 (x - 1) > x + 5 \end{matrix}$

查看试题解析
21. 先化简，再求值：（1﹣ $\frac{1}{x + 2}$ ）÷ $\frac{x^{2} + 2 x + 1}{x + 2}$ ，其中x= $\sqrt{3}$ ﹣1．

查看试题解析
22. 甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问：甲、乙每小时各做多少面彩旗？

查看试题解析
23. 一个不透明的口袋中装有2个红球（记为红球1、红球2），1个白球、1个黑球，这些球除颜色外都相同，将球搅匀．

(1)、从中任意摸出1个球，恰好摸到红球的概率是

(2)、先从中任意摸出一个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表），求两次都摸到红球的概率．

查看试题解析
24.
如图，在△ABC中，AB=AC，分别以B、C为圆心，BC长为半径在BC下方画弧．设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD

(1)、求证：AD平分∠BAC。

(2)、若BC=6，∠BAC=50°，求弧DE、弧DF的长度之和。（结果保留π）

查看试题解析
25.
如图，已知函数y= $\frac{k}{x}$ （x＞0）的图象经过点A、B，点B的坐标为（2，2）．过点A作AC⊥x轴，垂足为C，过点B作BD⊥y轴，垂足为D，AC与BD交于点F．一次函数y=ax+b的图象经过点A、D，与x轴的负半轴交于点E

(1)、若AC= $\frac{3}{2}$ OD，求a、b的值。

(2)、若BC∥AE，求BC的长。

查看试题解析
26.
如图，已知AD是△ABC的角平分线，⊙O经过A、B、D三点．过点B作BE∥AD，交⊙O于点E，连接ED。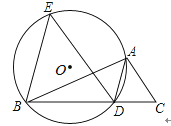

(1)、求证：ED∥AC

(2)、若BD=2CD，设△EBD的面积为S₁ ， △ADC的面积为S₂ ，且S₁²﹣16S₂+4=0，求△ABC的面积

查看试题解析
27.
如图，已知二次函数y=x²+（1﹣m）x﹣m（其中0＜m＜1）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，对称轴为直线l．设P为对称轴l上的点，连接PA、PC，PA=PC

(1)、∠ABC的度数为

(2)、求P点坐标（用含m的代数式表示）

(3)、在坐标轴上是否存在着点Q（与原点O不重合），使得以Q、B、C为顶点的三角形与△PAC相似，且线段PQ的长度最小？如果存在，求出所有满足条件的点Q的坐标；如果不存在，请说明理由．

查看试题解析
28.
如图，在矩形ABCD中，AD=acm，AB=bcm（a＞b＞4），半径为2cm的⊙O在矩形内且与AB、AD均相切，现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动．⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动，已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．

(1)、如图①，点P从A→B→C→D，全程共移动了 cm（用含a、b的代数式表示）

(2)、如图①，已知点P从A点出发，移动2s到达B点，继续移动3s，到达BC的中点，若点P与⊙O的移动速度相等，求在这5s时间内圆心O移动的距离

(3)、如图②，已知a=20，b=10，是否存在如下情形：当⊙O到达⊙O₁的位置时（此时圆心O₁在矩形对角线BD上），DP与⊙O₁恰好相切？请说明理由．

查看试题解析

通话时间x/min	0＜x≤5	5＜x≤10	10＜x≤15	15＜x≤20
频数（通话次数）	20	16	9	5