2015年江苏省南京市中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、选择题：本大题共6小题，每小题2分，共12分

1. 计算：|﹣5+3|的结果是（　　）

A、-2 B、2 C、-8 D、8

查看试题解析
2. 计算（﹣xy³）²的结果是（　　）

A、x²y⁶ B、﹣x²y⁶ C、x²y⁹ D、﹣x²y⁹

查看试题解析
3.
如图，在△ABC中，DE∥BC， $\frac{A D}{D B}$ = $\frac{1}{2}$ ，则下列结论中正确的是（　　）

A、 $\frac{A E}{A C}$ = $\frac{1}{2}$ B、 $\frac{D E}{B C}$ = $\frac{1}{2}$ C、= $\frac{1}{3}$ D、= $\frac{1}{3}$

查看试题解析
4. 某市2013年底机动车的数量是2×10⁶辆，2014年新增3×10⁵辆，用科学记数法表示该市2014年底机动车的数量是（　　）

A、2.3×10⁵辆 B、3.2×10⁵辆 C、2.3×10⁶辆 D、3.2×10⁶辆

查看试题解析
5. 估计 $\frac{\sqrt{5} - 1}{2}$ 介于（　　）

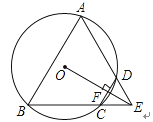
A、0.4与0.5之间 B、0.5与0.6之间 C、0.6与0.7之间 D、0.7与0.8之间

查看试题解析
6.
如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线BC于点M，切点为N，则DM的长为（　　）

A、 $\frac{13}{3}$ B、 $\frac{9}{2}$ C、 $\frac{4}{3} \sqrt{13}$ D、2 $\sqrt{5}$

查看试题解析

二、填空题（本大题共10小题，每小题2分，共20分）

7. 4的平方根是　；4的算术平方根是　．

查看试题解析
8. 若式子 $\sqrt{x + 1}$ 在实数范围内有意义，则x的取值范围是 .

查看试题解析
9. 计算 $\frac{\sqrt{5} \times \sqrt{15}}{\sqrt{3}}$ 的结果是 .

查看试题解析
10. 分解因式（a﹣b）（a﹣4b）+ab的结果是 .

查看试题解析
11. 不等式组 $\{\begin{matrix} 2 x + 1 > - 1 \\ 2 x + 1 < 3 \end{matrix}$ 的解集是 .

查看试题解析
12. 已知方程x²+mx+3=0的一个根是1，则它的另一个根是　， m的值是．

查看试题解析
13. 在平面直角坐标系中，点A的坐标是（2，﹣3），作点A关于x轴的对称点，得到点A′，再作点A′关于y轴的对称点，得到点A″，则点A″的坐标是 .

查看试题解析
14. 某工程队有14名员工，他们的工种及相应每人每月工资如下表所示：
工种
人数
每人每月工资/元
电工
5
7000
木工
4
6000
瓦工
5
5000
现该工程队进行了人员调整：减少木工2名，增加电工、瓦工各1名，与调整前相比，该工程队员工月工资的方差（填“变小”、“不变”或“变大”）．

查看试题解析
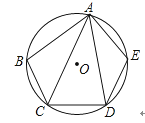
15.
如图，在⊙O的内接五边形ABCDE中，∠CAD=35°，则∠B+∠E= .

查看试题解析
16. 如图，过原点O的直线与反比例函数y₁ ， y₂的图象在第一象限内分别交于点A，B，且A为OB的中点，若函数y₁= $\frac{1}{x}$ ，则y₂与x的函数表达式是 .

查看试题解析

三、解答题：本大题共11小题，共88分

17.
解不等式2（x+1）﹣1≥3x+2，并把它的解集在数轴上表示出来．

查看试题解析
18. 解方程： $\frac{2}{x - 3}$ = $\frac{3}{x}$

查看试题解析
19. 计算： $(\frac{2}{a^{2} - b^{2}} - \frac{1}{a^{2} - a b}) \div \frac{a}{a + b}$

查看试题解析
20.
如图，△ABC中，CD是边AB上的高，且 $\frac{A D}{C D}$ = $\frac{C D}{B D}$

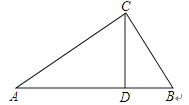(1)、求证：△ACD∽△CBD

(2)、求∠ACB的大小

查看试题解析
21.
为了了解2014年某地区10万名大、中、小学生50米跑成绩情况，教育部门从这三类学生群体中各抽取了10%的学生进行检测，整理样本数据，并结合2010年抽样结果，得到下列统计图：

(1)、本次检测抽取了大、中、小学生共名，其中小学生名.

(2)、根据抽样的结果，估计2014年该地区10万名大、中、小学生中，50米跑成绩合格的中学生人数为名.

(3)、比较2010年与2014年抽样学生50米跑成绩合格率情况，写出一条正确的结论.

查看试题解析
22. 某人的钱包内有10元、20元和50元的纸币各1张，从中随机取出2张纸币．

(1)、求取出纸币的总额是30元的概率

(2)、找出总额超过51元的结果数，然后根据概率公式计算

查看试题解析
23.
如图，轮船甲位于码头O的正西方向A处，轮船乙位于码头O的正北方向C处，测得∠CAO=45°，轮船甲自西向东匀速行驶，同时轮船乙沿正北方向匀速行驶，它们的速度分别为45km/h和36km/h，经过0.1h，轮船甲行驶至B处，轮船乙行驶至D处，测得∠DBO=58°，此时B处距离码头O多远？（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）

查看试题解析
24.
如图，AB∥CD，点E，F分别在AB，CD上，连接EF，∠AEF、∠CFE的平分线交于点G，∠BEF、∠DFE的平分线交于点H．

(1)、求证：四边形EGFH是矩形

(2)、
小明在完成（1）的证明后继续进行了探索，过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD于点P，Q，得到四边形MNQP，此时，他猜想四边形MNQP是菱形，请在下列框中补全他的证明思路．

查看试题解析
25.
如图，在边长为4的正方形ABCD中，请画出以A为一个顶点，另外两个顶点在正方形ABCD的边上，且含边长为3的所有大小不同的等腰三角形．（要求：只要画出示意图，并在所画等腰三角形长为3的边上标注数字3）

查看试题解析
26.
如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．

(1)、求证：∠A=∠AEB

(2)、连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形

查看试题解析
27.
某企业生产并销售某种产品，假设销售量与产量相等，如图中的折线ABD、线段CD分别表示该产品每千克生产成本y₁（单位：元）、销售价y₂（单位：元）与产量x（单位：kg）之间的函数关系．

(1)、请解释图中点D的横坐标、纵坐标的实际意义

(2)、求线段AB所表示的y₁与x之间的函数表达式

(3)、当该产品产量为多少时，获得的利润最大？最大利润是多少？

查看试题解析

工种	人数	每人每月工资/元
电工	5	7000
木工	4	6000
瓦工	5	5000