湖南省永州市新田县2019年中考数学一模试卷
试卷更新日期：2020-05-11 类型：中考模拟
一、选择题
-
1. 计算（﹣3）×（﹣4）的结果等于（ ）A、12 B、﹣12 C、-7 D、﹣42. 据《经济日报》2018年5月21日报道：目前，世界集成电路生产技术水平最高已达到7nm（1nm=10﹣9m），主流生产线的技术水平为14～28nm，中国大陆集成电路生产技术水平最高为28nm．将28nm用科学记数法可表示为（ ）
A、28×10﹣9m B、2.8×10﹣8m C、28×109m D、2.8×108m3. 把x3﹣16x分解因式，结果正确的是（ ）A、x(x2-16) B、x(x-4)2 C、x(x+4)2 D、x(x+4)(x-4)4. 如图是由5个大小相同的正方体搭成的几何体，这个几何体的俯视图是（ ）
A、
B、
C、
D、
5. 若等腰三角形的顶角为70°，则它的底角度数为（ ）A、400 B、500 C、550 D、6006. 根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图．
根据图所提供的信息，若要推荐一位成绩较稳定的选手去参赛，应推荐（ ）
A、李飞或刘亮 B、李飞 C、刘亮 D、无法确定7. 下列说法正确的是（ ）A、菱形的对角线垂直且相等 B、到线段两端点距离相等的点，在线段的垂直平分线上 C、角的平分线就是角的对称轴 D、形状相同的两个三角形就是全等三角形8. 若一元二次方程x2﹣2x-m=0有两个不相同的实数根，则实数m的取值范围是（ ）A、m≥-1 B、m≤1 C、m＞-1 D、m＜-19. 如图所示，在平面直角坐标系中，已知点A（2，4），过点A作AB⊥x轴于点B．将△AOB以坐标原点O为位似中心缩小为原图形的 ，得到△COD，则CD的长度是（ ）
A、1 B、2 C、2 D、10. 阅读理解：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（ ）
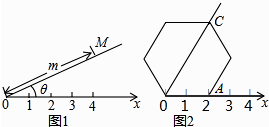A、（60°，4） B、（45°，4） C、（60°，2 ） D、（50°，2 ）二、填空题
-
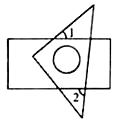
11. 使表达式 有意义的x的取值范围是 ．12. 化简： =.13. 将一个含有45°角的直角三角板摆放在矩形上，如图所示，若∠1=40°，则∠2= ．
14. 如图，AB为⊙O的直径，CD是⊙O的弦，∠ADC=25°，则∠CAB的度数为 ．
15. 一圆锥的侧面展开后是扇形，该扇形的圆心角为120°，半径为6cm，则此圆锥的表面积为cm2 ．16. 为了改善生态环境，防止水土流失，红旗村计划在荒坡上种树960棵，由于青年志愿者支援，实际每天种树的棵数是原计划的2倍，结果提前4天完成任务，则原计划每天种树的棵数是.17. 从﹣1、0、 、0.3、π、 这六个数中任意抽取一个，抽取到无理数的概率为 ．18. 任何大于1的正整数m的三次幂均可分裂成m个连续奇数的和．如：23=3+5、33=7+9+11、43=13+15+17+19……依此规律，若m3分裂后其中有一个奇数是2019，则m的值是.三、综合题
-
19. 计算：|﹣5|+（﹣1）2019﹣ ﹣ ．20. 解不等式组 ，并把它的解集在数轴上表示出来．
21. 为了了解居民的环保意识，社区工作人员在光明小区随机抽取了若干名居民开展主题为“打赢蓝天保卫战”的环保知识有奖问答活动，并用得到的数据绘制了如图条形统计图（得分为整数，满分为10分，最低分为6分）请根据图中信息，解答下列问题：
(1)、本次调查一共抽取了名居民；
(2)、求本次调查获取的样本数据的平均数、众数和中位数；
(3)、社区决定对该小区500名居民开展这项有奖问答活动，得10分者设为“一等奖”，请你根据调查结果，帮社区工作人员估计需准备多少份“一等奖”奖品？
22. 如图，在正方形ABCD中，AF=BE，AE与DF相交于于点O．
(1)、求证：△DAF≌△ABE；(2)、求∠AOD的度数；(3)、若AO=4，DF=10，求 的值.23. 如图，在平面直角坐标系中，一次函数y=k1x+b的图象与反比例函数y= 的图象交于A（4，﹣2）、B（﹣2，n）两点，与x轴交于点C．
(1)、求k2 ， n的值；
(2)、请直接写出不等式k1x+b< 的解集；(3)、将x轴下方的图象沿x轴翻折，点A落在点A′处，连接A′B，A′C，求△A′BC的面积．24. 如图，AB为⊙O的直径，C为⊙O上一点，∠ABC的平分线交⊙O于点D，DE⊥BC于点E．
(1)、试判断DE与⊙O的位置关系，并说明理由；(2)、过点D作DF⊥AB于点F，若BE=3 ，DF=3，求图中阴影部分的面积．25. 如图①，在平面直角坐标系xOy 中，抛物线y=ax2+bx+3经过点A(-1，0) 、B(3，0) 两点，且与y轴交于点C.
(1)、求抛物线的表达式；(2)、如图②，用宽为4个单位长度的直尺垂直于x轴，并沿x轴左右平移，直尺的左右两边所在的直线与抛物线相交于P、 Q两点（点P在点Q的左侧），连接PQ，在线段PQ上方抛物线上有一动点D，连接DP、DQ.①若点P的横坐标为 ，求△DPQ面积的最大值，并求此时点D 的坐标；
②直尺在平移过程中，△DPQ面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由.
26.已知点P是线段AB上与点A不重合的一点，且AP＜PB．AP绕点A逆时针旋转角α（0°＜α≤90°）得到AP1 ， BP绕点B顺时针也旋转角α得到BP2 ， 连接PP1、PP2 ．
(1)、如图1，当α=90°时，求∠P1PP2的度数；
(2)、如图2，当点P2在AP1的延长线上时，求证：△P2P1P∽△P2PA；
(3)、如图3，过BP的中点E作l1⊥BP，过BP2的中点F作l2⊥BP2 ， l1与l2交于点Q，连接PQ，求证：P1P⊥PQ．