湖南省益阳市南县2019年中考数学学业水平考试

试卷更新日期：2020-05-11 类型：水平会考

进入出卷网下载

一、选择题

1. ﹣6的倒数是（）

A、﹣ $\frac{1}{6}$ B、 $\frac{1}{6}$ C、﹣6 D、6

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{{(- 2)}^{2}}$ ＝﹣2 B、(2 $\sqrt{3}$ )²＝6 C、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$

查看试题解析
3. 下列几何体中，其侧面展开图为扇形的是（）

A、 B、 C、 D、

查看试题解析
4. 解分式方程 $\frac{x}{2 x - 1} + \frac{2}{1 - 2 x} = 3$ 时，去分母化为一元一次方程，正确的是（）

A、x+2＝3 B、x﹣2＝3 C、x﹣2＝3(2x﹣1) D、x+2＝3(2x﹣1)

查看试题解析
5. 下列函数中，y总随x的增大而减小的是（）

A、y＝4x B、y＝﹣4x C、y＝x﹣4 D、y＝x²

查看试题解析
6. 已知一组数据5，8，8，9，10，以下说法不正确的是（）

A、平均数是8 B、众数是8 C、中位数是8 D、方差是8

查看试题解析
7. 已知M、N是线段AB上的两点，AM＝MN＝2，NB＝1，以点A为圆心，AN长为半径画弧；再以点B为圆心，BM长为半径画弧，两弧交于点C，连接AC，BC，则△ABC一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
8. 南洞庭大桥是南益高速公路上的重要桥梁，小芳同学在校外实践活动中对此开展测量活动．如图，在桥外一点A测得大桥主架与水面的交汇点C的俯角为α，大桥主架的顶端D的仰角为β，已知测量点与大桥主架的水平距离AB＝a，则此时大桥主架顶端离水面的高CD为（）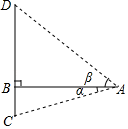

A、asinα+asinβ B、acosα+acosβ C、atanα+atanβ D、 $\frac{a}{\tan α} + \frac{a}{\tan β}$

查看试题解析
9. 如图，PA、PB为圆O的切线，切点分别为A、B，PO交AB于点C，PO的延长线交圆O于点D，下列结论不一定成立的是（）

A、PA＝PB B、∠BPD＝∠APD C、AB⊥PD D、AB平分PD

查看试题解析
10. 已知二次函数y＝ax²+bx+c的图象如图所示，下列结论：①ac＜0，②b﹣2a＜0，③b²﹣4ac＜0，④a﹣b+c＜0，正确的是（）

A、①② B、①④ C、②③ D、②④

查看试题解析

二、填空题

11. 国家发改委发布信息，到2019年12月底，高速公路电子不停车快速收费(ETC)用户数量将突破1.8亿，将180 000 000科学记数法表示为．

查看试题解析
12. 若一个多边形的内角和与外角和之和是900°，则该多边形的边数是．

查看试题解析
13. 不等式组 ${\begin{array}{l} x - 1 < 0 \\ - x > 3 \end{array}$ 的解集为．

查看试题解析
14. 如图，直线AB∥CD，OA⊥OB，若∠1＝142°，则∠2＝度．

查看试题解析
15. 在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A'B'C'，使各顶点仍在格点上，则其旋转角的度数是．．

查看试题解析
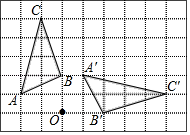16. 小蕾有某文学名著上、中、下各1册，她随机将它们叠放在一起，从上到下的顺序恰好为“上册、中册、下册”的概率是．

查看试题解析
17. 反比例函数 $y = \frac{k}{x}$ 的图象上有一点P(2，n)，将点P向右平移1个单位，再向下平移1个单位得到点Q，若点Q也在该函数的图象上，则k＝．

查看试题解析
18. 观察下列等式：
①3﹣2 $\sqrt{2}$ ＝( $\sqrt{2}$ ﹣1)² ， ②5﹣2 $\sqrt{6}$ ＝( $\sqrt{3}$ ﹣ $\sqrt{2}$ )² ， ③7﹣2 $\sqrt{12}$ ＝( $\sqrt{4}$ ﹣ $\sqrt{3}$ )² ，

…

请你根据以上规律，写出第6个等式．

查看试题解析

三、综合题

19. 计算： $4 \sin 60 ° + {(- 2019)}^{0} - {(\frac{1}{2})}^{- 1} - | - 2 \sqrt{3} |$ ．

查看试题解析
20. 化简： $(\frac{x^{2} + 4}{x} - 4) \div \frac{x^{2} - 4}{2 x}$ ．

查看试题解析
21. 已知，如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EAD．

查看试题解析
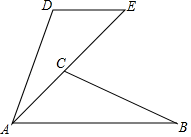22. 某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查，根据每车乘坐人数分为5类，每车乘坐1人、2人、3人、4人、5人分别记为A、B、C、D、E，由调查所得数据绘制了如图所示的不完整的统计图表．
类别
频率
A
m
B
0.35
C
0.20
D
n
E
0.05

(1)、求本次调查的小型汽车数量及m，n的值；

(2)、补全频数分布直方图；

(3)、若某时段通过该路段的小型汽车数量为5000辆，请你估计其中每车只乘坐1人的小型汽车数量．

查看试题解析
23. 如图，在Rt△ABC中，M是斜边AB的中点，以CM为直径作圆O交AC于点N，延长MN至D，使ND＝MN，连接AD、CD，CD交圆O于点E．

(1)、判断四边形AMCD的形状，并说明理由；

(2)、求证：ND＝NE；

(3)、若DE＝2，EC＝3，求BC的长．

查看试题解析
24. 为了提高农田利用效益，某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾•稻”轮作模式．某农户有农田20亩，去年开始实施“虾•稻”轮作，去年出售小龙虾每千克获得的利润为32元(利润＝售价﹣成本)．由于开发成本下降和市场供求关系变化，今年每千克小龙虾的养殖成本下降25%，售价下降10%，出售小龙虾每千克获得利润为30元．

(1)、求去年每千克小龙虾的养殖成本与售价；

(2)、该农户今年每亩农田收获小龙虾100千克，若今年的水稻种植成本为600元/亩，稻谷售价为25元/千克，该农户估计今年可获得“虾•稻”轮作收入不少于8万元，则稻谷的亩产量至少会达到多少千克？

查看试题解析
25. 在平面直角坐标系xOy中，顶点为A的抛物线与x轴交于B、C两点，与y轴交于点D，已知A(1，4)，B(3，0)．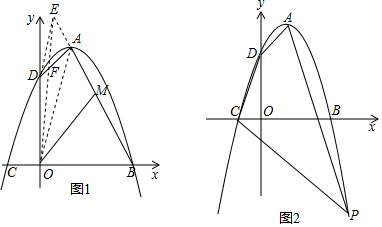

(1)、求抛物线对应的二次函数表达式；

(2)、探究：如图1，连接OA，作DE∥OA交BA的延长线于点E，连接OE交AD于点F，M是BE的中点，则OM是否将四边形OBAD分成面积相等的两部分？请说明理由；

(3)、应用：如图2，P(m，n)是抛物线在第四象限的图象上的点，且m+n＝﹣1，连接PA、PC，在线段PC上确定一点M，使AN平分四边形ADCP的面积，求点N的坐标．提示：若点A、B的坐标分别为(x₁ ， y₁)、(x₂ ， y₂)，则线段AB的中点坐标为( $\frac{x_{1} + x_{2}}{2}$ ， $\frac{y_{1} + y_{2}}{2}$ )．

查看试题解析
26. 如图，在平面直角坐标系xOy中，矩形ABCD的边AB＝4，BC＝6．若不改变矩形ABCD的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y轴的正半轴上随之上下移动．

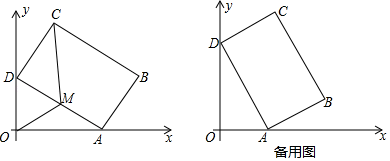(1)、当∠OAD＝30°时，求点C的坐标；

(2)、设AD的中点为M，连接OM、MC，当四边形OMCD的面积为 $\frac{21}{2}$ 时，求OA的长；

(3)、当点A移动到某一位置时，点C到点O的距离有最大值，请直接写出最大值，并求此时cos∠OAD的值．

查看试题解析

类别	频率
A	m
B	0.35
C	0.20
D	n
E	0.05