湖南省益阳市2019年中考数学二模试卷
试卷更新日期:2020-05-11 类型:中考模拟
一、选择题
-
1. 誉为全国第三大露天碑林的“浯溪碑林”,摩崖上铭刻着500多方古今名家碑文,其中悬针篆文具有较高的历史意义和研究价值,下面四个悬针篆文文字明显不是轴对称图形的是( )A、
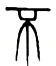 B、
B、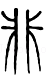 C、
C、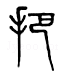 D、
D、 2. 要使分式 有意义,则x应满足的条件是( )A、x>0 B、x≠0 C、x>﹣1 D、x≠﹣13. 按照如图所示的操作步骤,若输入的值为3,则输出的值为( )
2. 要使分式 有意义,则x应满足的条件是( )A、x>0 B、x≠0 C、x>﹣1 D、x≠﹣13. 按照如图所示的操作步骤,若输入的值为3,则输出的值为( ) A、54 B、55 C、60 D、614. 如图,DE是线段AC的垂直平分线,下列结论一定成立的是( )
A、54 B、55 C、60 D、614. 如图,DE是线段AC的垂直平分线,下列结论一定成立的是( )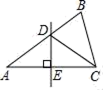 A、DE=BD B、∠BCD=∠A C、∠B>2∠A D、2∠BAC=180°﹣2∠ADE5. 矩形的对角线长为20,两邻边之比为3:4,则矩形的面积为( )A、56 B、192 C、20 D、以上答案都不对6. 为了解小学生的体能情况,抽取了某小学同年级50名学生进行1分钟跳绳测试,将所得数据整理后,画出如图所示的频数分布直方图(各组只含最小值,不含最大值).已知图中从左到右各组的频率分别是a , 0.3,0.4,0.2,设跳绳次数不低于100次的学生有b人,则a , b的值分别是( )
A、DE=BD B、∠BCD=∠A C、∠B>2∠A D、2∠BAC=180°﹣2∠ADE5. 矩形的对角线长为20,两邻边之比为3:4,则矩形的面积为( )A、56 B、192 C、20 D、以上答案都不对6. 为了解小学生的体能情况,抽取了某小学同年级50名学生进行1分钟跳绳测试,将所得数据整理后,画出如图所示的频数分布直方图(各组只含最小值,不含最大值).已知图中从左到右各组的频率分别是a , 0.3,0.4,0.2,设跳绳次数不低于100次的学生有b人,则a , b的值分别是( ) A、0.2,30 B、0.3,30 C、0.1,20 D、0.1,307. 一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( )
A、0.2,30 B、0.3,30 C、0.1,20 D、0.1,307. 一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( ) A、 B、 C、4 D、2+8. 如图,火车匀速通过隧道(隧道长等于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是( )
A、 B、 C、4 D、2+8. 如图,火车匀速通过隧道(隧道长等于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,空心卷筒纸的高度为12cm,外径(直径)为10cm,内径为4cm,在比例尺为1:4的三视图中,其主视图的面积是( )
9. 如图,空心卷筒纸的高度为12cm,外径(直径)为10cm,内径为4cm,在比例尺为1:4的三视图中,其主视图的面积是( ) A、
A、 cm2
B、
cm2
B、 cm2
C、
cm2
C、 cm2
D、
cm2
D、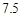 cm2
10. 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2 , 四边形ABCD面积是11cm2 , 则①②③④四个平行四边形周长的总和为( )
cm2
10. 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2 , 四边形ABCD面积是11cm2 , 则①②③④四个平行四边形周长的总和为( ) A、48cm B、36cm C、24cm D、18cm
A、48cm B、36cm C、24cm D、18cm二、填空题
-
11. 因式分解:m2﹣4n2= .12. 2018年5月18日,益阳新建西流湾大桥竣工通车,如图,从沅江A地到资阳B地有两条路线可走,从资阳B地到益阳火车站可经会龙山大桥或西流湾大桥或龙洲大桥到达,现让你随机选择一条从沅江A地出发经过资阳B地到达益阳火车站的行走路线,那么恰好选到经过西流湾大桥的路线的概率是 .
 13. 某学习小组为了探究函数y=x2﹣|x|的图象和性质,根据以往学习函数的经验,列表确定了该函数图象上一些点的坐标,表格中的m=.
13. 某学习小组为了探究函数y=x2﹣|x|的图象和性质,根据以往学习函数的经验,列表确定了该函数图象上一些点的坐标,表格中的m=.x
…
﹣2
﹣1.5
﹣1
﹣0.5
0
0.5
1
1.5
2
…
y
…
2
0.75
0
﹣0.25
0
﹣0.25
0
m
2
…
14. 从1978年12月18日党的十一届三中全会决定改革开放到如今已经40周年了,我国GDP(国内生产总值)从1978年的1495亿美元到2017年已经达到了122400亿美元,全球排名第二,将数字用a×10b的科学记数法表示,则b的值为 .15. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB , 他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一条直线上.已知纸板的两条边DE=70cm , EF=30cm , 测得AC= m , BD=9m , 求树高AB . 16. 如图,AB是⊙O的直径,BD , CD分别是过⊙O上点B , C的切线,且∠BDC=110°.连接AC , 则∠A的度数是°.
16. 如图,AB是⊙O的直径,BD , CD分别是过⊙O上点B , C的切线,且∠BDC=110°.连接AC , 则∠A的度数是°. 17. 如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE , 如果正方形ABCD的边长是2,那么△EPF的面积是 .
17. 如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE , 如果正方形ABCD的边长是2,那么△EPF的面积是 .
三、综合题
-
18. ( )2﹣|1﹣ |﹣tan45°+(π﹣1978)0 .19. 先化简再求值: 其中20. 如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF , 交点为G .
求证:AE⊥BF .
 21. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
21. 垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩(分)
7
6
8
7
7
5
8
7
8
7
 (1)、写出运动员甲测试成绩的众数和中位数;(2)、在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)22. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC , 交AB的延长线于点F , 连接DA .
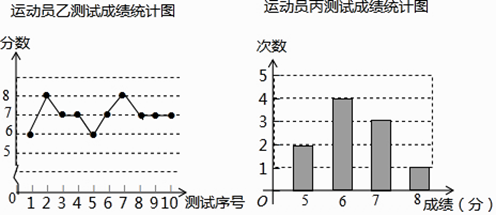
(1)、写出运动员甲测试成绩的众数和中位数;(2)、在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)(3)、甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)22. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC , 交AB的延长线于点F , 连接DA . (1)、求证:EF为半圆O的切线;(2)、若DA=DF=6 ,求阴影区域的面积.(结果保留根号和π)23. 贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
(1)、求证:EF为半圆O的切线;(2)、若DA=DF=6 ,求阴影区域的面积.(结果保留根号和π)23. 贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).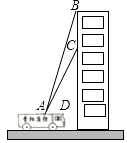 24. 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y= (x>0)的图象经过线段OC的中点A , 交DC于点E , 交BC于点F . 设直线EF的解析式为y=k2x+b .
24. 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y= (x>0)的图象经过线段OC的中点A , 交DC于点E , 交BC于点F . 设直线EF的解析式为y=k2x+b . (1)、求反比例函数和直线EF的解析式;(2)、求△OEF的面积;(3)、请结合图象直接写出不等式k2x+b﹣ >0的解集.25. 在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)、求反比例函数和直线EF的解析式;(2)、求△OEF的面积;(3)、请结合图象直接写出不等式k2x+b﹣ >0的解集.25. 在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.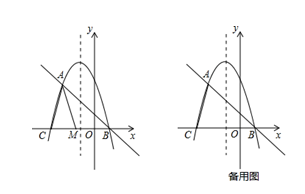 (1)、填空:该抛物线的“衍生直线”的解析式为 , 点A的坐标为 , 点B的坐标为 ;(2)、如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;(3)、当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
(1)、填空:该抛物线的“衍生直线”的解析式为 , 点A的坐标为 , 点B的坐标为 ;(2)、如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;(3)、当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.