湖南省邵阳市2019年中考数学三模试卷

试卷更新日期：2020-05-11 类型：中考模拟

进入出卷网下载

一、选择题

1. 估计 $\sqrt{5}$ +1的值，应在（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
2. 下列运算正确的是（）

A、 $x - 2 x = - x$ B、 $2 x - y = - x y$ C、 $x^{2} + x^{2} = x^{4}$ D、 ${(x - 1)}^{2} = x^{2} - 1$

查看试题解析
3. 如图，直线AB∥CD，则下列结论正确的是（）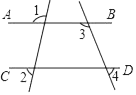

A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3+∠4=180°

查看试题解析
4. 如图是某圆锥的主视图和左视图，该圆锥的侧面积是（）

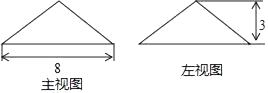A、25π B、24π C、20π D、15π

查看试题解析
5. 顺次连接矩形的四边形中点所得的四边形一定是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
6. 《九章算术》是中国古代数学专著在数学上有其独到的成就，不仅最早提到了分数问题，首先记录了“盈不足”等问题．如有一道阐述“盈不足”的问题，原文如下：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数、鸡价各几何？译文为：现有若干人合伙出钱买鸡，如果每人出9文钱，就会多11文钱；如果每人出6文钱又会缺16文钱，问买鸡的人数、鸡的价格各是多少？通过计算可得买鸡的人数是（）

A、6 B、7 C、8 D、9

查看试题解析
7. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
8. 下列说法正确的是（）

A、调查舞水河的水质情况，采用抽样调查的方式 B、数据2.0，﹣2，1，3的中位数是﹣2 C、可能性是99%的事件在一次实验中一定会发生 D、从2000名学生中随机抽取100名学生进行调查，样本容量为2000名学生

查看试题解析
9. 已知抛物线y＝ $x^{2}$ ﹣x﹣1与x轴的一个交点为(m，0)，则代数式m²﹣m+2019的值为（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
10. 如图，木工师傅在板材边角处作直角时，往往使用“三弧法”，其作法是：
；（1）作线段 $A B$ ，分别以 $A ， B$ 为圆心，以 $A B$ 长为半径作弧，两弧的交点为 $C$ ；（2）以 $C$ 为圆心，仍以 $A B$ 长为半径作弧交 $A C$ 的延长线于点 $D$ ；（3）连接 $B D ， B C$ 下列说法不正确的是（）

A、 $∠ C B D = 30^{\circ}$ B、 $S_{Δ B D C} = \frac{\sqrt{3}}{4} A B^{2}$ C、点 $C$ 是 $Δ A B D$ 的外心 D、 $\sin^{2} A + \cos^{2} D = 1$

查看试题解析

二、填空题

11. 因式分解： $a^{2} (a - b) - 4 (a - b)$ ＝.

查看试题解析
12. 据统计，2017年长沙市地区生产总值约为10200亿元，经济总量迈入“万亿俱乐部”数据10200用科学记数法表示为．

查看试题解析
13. 若反比例函数 $y = \frac{2 - k}{x}$ 的图象位于第二、四象限，则 $k$ 的取值范围是.

查看试题解析
14. 甲、乙两名同学的5次射击训练成绩（单位：环）如下表．
甲
7
8
9
8
8
乙
6
10
9
7
8
比较甲、乙这5次射击成绩的方差S_甲² ， S_乙² ，结果为：S_甲²S_乙² ．（选填“＞”“=”或“＜“）

查看试题解析
15. 如图，在△ABC中，D为AB边上的一点，要使△ABC～△AED成立，还需要添加一个条件为．

查看试题解析
16. 如图，已知▱ABCD中，DE是∠ADC的角平分线，交BC于点E ，且BE＝CE ，若AD＝10 cm，则▱ABCD的周长为 cm.

查看试题解析
17. x的3倍大于5，且x的一半与1的差小于或等于2，则x的取值范围是．

查看试题解析
18. 如图，在矩形ABCD中，AB=4，AD=3，矩形内部有一动点P满足S_△_PAB= $\frac{1}{3}$ S_矩形_ABCD ，则点P到A、B两点的距离之和PA+PB的最小值为.

查看试题解析

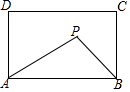
三、综合题

19. 计算： $\sqrt{12} - | 1 - \sqrt{3} | + {(7 + π)}^{0}$ ．

查看试题解析
20. 先化简，再求值： $(x - 2 + \frac{8 x}{x - 2}) \div \frac{x + 2}{2 x - 4}$ ，其中 $x = - \frac{1}{2}$ ．

查看试题解析
21. 如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点．

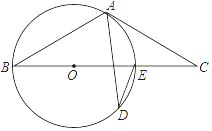(1)、若∠ADE=25°，求∠C的度数；

(2)、若AB=AC，CE=2，求⊙O半径的长．

查看试题解析
22. 如图，某测量小组为了测量山BC的高度，在地面A处测得山顶B的仰角45°，然后沿着坡度为 $i = 1 ： \sqrt{3}$ 的坡面AD走了200米达到D处，此时在D处测得山顶B的仰角为60°，求山高BC（结果保留根号）．

查看试题解析
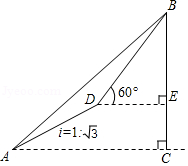23. 张老师为了了解班级学生完成数学课前预习的具体情况，对本班部分学生进行了为期半个月的跟踪调查．他将调查结果分为四类：A：很好；B：较好；C：一般；D：较差，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

(1)、请计算出A类男生和C类女生的人数，并将条形统计图补充完整．

(2)、为了共同进步，张老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习，请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率．

查看试题解析
24. 为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台.假定该设备的年销售量y(单位：台)和销售单价 $x$ (单位：万元)成一次函数关系.

(1)、求年销售量 $y$ 与销售单价 $x$ 的函数关系式；

(2)、根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?

查看试题解析
25. 在△ABC中，∠ABC=90°，AB=BC=4，点M是线段BC的中点，点N在射线MB上，连接AN，平移△ABN，使点N移动到点M，得到△DEM（点D与点A对应，点E与点B对应），DM交AC于点P．

(1)、若点N是线段MB的中点，如图1．
①依题意补全图1；

②求DP的长；

(2)、若点N在线段MB的延长线上，射线DM与射线AB交于点Q，若MQ=DP，求CE的长．

查看试题解析
26. 如图，抛物线y=ax²+bx经过△OAB的三个顶点，其中点A（1， $\sqrt{3}$ ），点B（3，﹣ $\s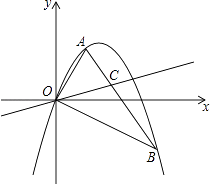qrt{3}$ ），O为坐标原点．

(1)、求这条抛物线所对应的函数表达式；

(2)、若P（4，m），Q（t，n）为该抛物线上的两点，且n＜m，求t的取值范围；

(3)、若C为线段AB上的一个动点，当点A，点B到直线OC的距离之和最大时，求∠BOC的大小及点C的坐标．

查看试题解析

甲	7	8	9	8	8
乙	6	10	9	7	8