湖南省常德市2019年中考数学二模试卷

试卷更新日期：2020-05-11 类型：中考模拟

进入出卷网下载

一、选择题

1. 算式 $(- 3) \times | - 4 | - | - 5 |$ 计算后的结果为（）

A、17 B、 $- 7$ C、 $- 5$ D、 $- 17$

查看试题解析
2. 某县有近6千名考生参加中考，为了解本次中考的数学成绩，从中抽取100名考生的数学成绩进行统计分析，以下说法正确的是（）

A、这100名考生是总体的一个样本 B、近6千名考生是总体 C、每位考生的数学成绩是个体 D、100名学生是样本容量

查看试题解析
3. 下列计算正确的是（）

A、a²+a²=2a⁴ B、（2a）²=4a C、 $\sqrt{3} \times \sqrt{3} = 3$ D、 $\sqrt{12} \div 3 = 2$

查看试题解析
4. 甲车行驶30千米与乙车行驶40千米所用时间相同，已知乙车每小时比甲车多行驶15千米，设甲车的速度为x千米/小时，依据题意列方程正确的是（）

A、 $\frac{30}{x} = \frac{40}{x - 15}$ B、 $\frac{30}{x - 15} = \frac{40}{x}$ C、 $\frac{30}{x} = \frac{40}{x + 15}$ D、 $\frac{30}{x + 15} = \frac{40}{x}$

查看试题解析
5. 函数y=x+1、y=- $\frac{2}{x}$ 、y=x²中，当x＞0时，y随x增大而增大的函数共有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6.
如图，在Rt△ABC中，∠B=90°，AB=6，BC=8，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE的最小值是（　　）

A、10 B、8 C、6 D、5

查看试题解析
7. 二次函数y=-x²+bx+c的图象如图所示，下列几个结论：①对称轴为直线x=2；②当y≥0时，x＜0或x＞4：③函数表达式为y=-x²+4x；④当x≤0时，y随x的增大而增大．其中正确的结论有（）

A、①②③④ B、①②③ C、①③④ D、②③④

查看试题解析
8. 观察下列一组图形中的个数，其中第1个图中共有4个点，第2个图中共有10个点，第3个图中共有19个点，……，按此规律第5个图中共有点的个数是（）

A、31 B、46 C、51 D、66

查看试题解析

二、填空题

9. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
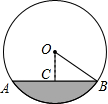
10. 不等式组： ${\begin{array}{l} 4 x - 1 < 7 \\ 2 x + 3 \geq 1 \end{array}$ 的解集．

查看试题解析
11. 一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是．

查看试题解析
12. 如图，△ABC中，BD和CE是两条高，如果∠A＝45°，则 $\frac{D E}{B C}$ ＝．

查看试题解析
13. 直线y=kx+b经过A（2，1）、B（-1，2）两点，则不等式 $\frac{1}{2} x$ ＞kx+b＞-2的解集为．

查看试题解析
14. 已知△ABC中，AB=AC=4 $\sqrt{3}$ ，高AD=4，则△ABC的外接圆半径是．

查看试题解析
15. 直线y=x+a-3与双曲线y= $\frac{4}{x}$ 交于A，B两点，则当线段A，B的长度取最小值时，a的值为．

查看试题解析
16. a是不为1的有理数，我们把 $\frac{1}{1 - a}$ 称为的差倒数．如：2的差倒数是 $\frac{1}{1 - 2}$ =-1，-1的差倒数是 $\frac{1}{1 - (- 1)} = \frac{1}{2}$ ．已知a₁=- $\frac{1}{3}$ ，a₂是a₁的差倒数，a₃是a₂的差倒数，a₄是a₃的差倒数，…，依此类推，则a₂₀₁₉= ．

查看试题解析

三、综合题

17. 计算：（ $\frac{1}{2}$ ）^-1-2cos30°+ $\sqrt{27}$ +（2-π）⁰

查看试题解析
18. 已知a，b，c为实数，且有a=10-b，c²=ab-25，求 $\frac{a}{b}$ 的值．

查看试题解析
19. 先化简，再求值： $(1 + \frac{x^{2} - 1}{x^{2} - 2 x + 1}) \div \frac{1}{x - 1}$ ，其中 $x = \frac{1}{2}$ ．

查看试题解析
20. 已知甲同学手中藏有三张分别标有数字 $\frac{1}{2} ， \frac{1}{4} ， 1$ 的卡片，乙同学手中藏有三张分别标有数字1，3，2的卡片，卡片外形相同.现从甲乙两人手中各任取一张卡片，并将它们的数字分别记为 $a ， b$ .

(1)、请你用树形图或列表法列出所有可能的结果.

(2)、现制定这样一个游戏规则：若所选出的 $a ， b$ 能使得 $a x^{2} + b x + 1 = 0$ 有两个不相等的实数根，则甲获胜；否则乙获胜.请问这样的游戏规则公平吗？请你用概率知识解释

查看试题解析
21. “农民也可以报销医疗费了！”这是我区推行新型农村医疗合作的成果．村民只要每人每年交10元钱，就可以加入合作医疗，每年先由自己支付医疗费，年终时可得到按一定比例返回的返回款，这一举措极大地增强了农民抵御大病风险的能力．小华与同学随机调查了他们乡的一些农民，根据收集到的数据绘制了以下的统计图．根据以上信息，解答以下问题：

(1)、本次调查了多少村民？被调查的村民中，有多少人参加合作医疗得到了返回款？

(2)、该乡若有10000村民，请你估计有多少人参加了合作医疗？要使两年后参加合作医疗的人数增加到9680人，假设这两年的年增长率相同，求这个年增长率．

查看试题解析
22. 如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且 $\overset{⌢}{A E} = \overset{⌢}{D E}$ ，过点E作EF⊥BC于点F，延长FE和BA的延长线交与点G．

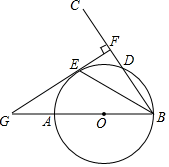(1)、证明：GF是⊙O的切线；

(2)、若AG＝6，GE＝6 $\sqrt{2}$ ，求△GOE的面积．

查看试题解析
23. 如图，直线y= -x+3与x轴，y轴分别相交于点B、C，经过B、C两点的抛物线 $y = a x^{2} + b x + c$ 与x轴的另一交点为A，顶点为P，且对称轴为直线x=2．

(1)、求A点的坐标；

(2)、求该抛物线的函数表达式；

(3)、连结AC．请问在x轴上是否存在点Q，使得以点P、B、Q为顶点的三角形与△ABC 相似，若存在，请求出点Q的坐标；若不存在，请说明理由．

查看试题解析
24. 如图，在Rt△ABC中，∠ACB=90°，AC=BC．点P为AB边上一点，Q为BC边上一点，且∠BPQ=∠APC，过点A作AD⊥PC，交BC于点D，直线AD分别交直线PC、PQ于E、F．

(1)、求证：∠FDQ=∠FQD；

(2)、把△DFQ沿DQ边翻折，点F刚好落在AB边上点G，设PC分别交GQ、GD于M、N，试判定MN与EN的数量关系，并给予证明．

查看试题解析
25. 近年来，雾霾天气给人们的生活带来很大影响，空气质量问题倍受人们关注，某学校计划在教室内安装空气净化装置，需购进A、B两种设备，已知：购买1台A种设备和2台B种设备需要3.5万元；购买2台A种设备和1台B种设备需要2.5万元.

(1)、求每台A种、B种设备各多少万元？

(2)、根据学校实际，需购进A种和B种设备共30台，总费用不超过30万元，请你通过计算，求至少购买A种设备多少台？

查看试题解析
26. 有一款如图（1）所示的健身器材，可通过调节AB的长度来调节椅子的高度，其平面示意图如图（2）所示，经测量，AD与DE的夹角为75°，AC与AD的夹角为45°，且DE∥AB．现调整AB的长度，当∠BCA为75°时测得点C到地面的距离为25cm．请求出此时AB的长度（结果保留根号）．

查看试题解析