吉林省白城市通榆县2020年中考数学五模试卷
试卷更新日期：2020-05-11 类型：中考模拟
一、单项选择题(每小题2分，共12分)
-
1. 已知∠A是锐角，tanA=1，那么∠A的度数是（ ）A、15° B、30° C、45° D、60°2. 二次函数y=-2(x+1)²-3的最大值为（ ）A、-1 B、-2 C、-3 D、-43. 如图是几种汽车轮毂的图案，绕中心旋转90°后能与原来的图案重合的是（ ）A、
B、
C、
D、
4. 如图是由5个完全相同的小正方体搭成的几何体，如果将小正方体A放到小正方体B的正上方，则它的（ ）
A、主视图会发生改变 B、俯视图会发生改变 C、左视图会发生改变 D、三种视图都会发生改变5. 已知OA，OB是圆Ｏ的半径，点C，D在圆O上，且OA∥BC，若∠ADC=26°，则∠B的度数为（ ）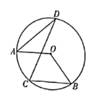
A、30° B、42° C、46° D、52°6. 反比例函数y= 在第一象限内的图像如图所示，则k的值可能是（ ）
A、3 B、5 C、6 D、8二、填空题(每小题3分，共24分)
-
7. 将一元二次方程x2+4x-1=0变形为(x+m)²=k的形式为 。8. 若关于x的一元二次方程9x2-6x+c=0有两个不相等的实数根，则c的取值范围是。9. 已知Rt△ABC∽Rt△A'B'C'，且∠C=∠C'=90°，若AC=3，BC=4，A'B'=10，则A'C'=。10.
若将等腰直角三角形AOB按如图所示放置，OB=2，则点A关于原点对称的点的坐标为 ．
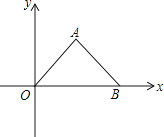11. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanB的值为.
12. 如图，设A(-2，y1)、B(1，y2)、C(2，y3)是抛物线y=-(x+1)²+m上的三点，则y1 ， y2 ， y3的大小关系为(用“>”连接)。
13. 如图，在一块长8m、宽6m的矩形绿地内，开辟出一块矩形的花圃，使花圃四周的绿地等宽，已知绿地的面积与花圃的面积相等，求花圃四周绿地的宽．设花圃四周绿地的宽为xm，可列方程为 (不需要化简)。
14. 如图，将半径为2、圆心角为90°的扇形BAC绕点A逆时针旋转，点B，C的对应点分别为点D，E。若点D在 上，则阴影部分的面积为。
三、解答题(每小题5分，共20分)
-
15. 小明要把一篇社会调查报告录入电脑，当他以100字/分钟的速度录入文字时，经过240分钟能完成录入。设他录入文字的速度为v字/分钟时，完成录入的时间为t分钟。求t与v之间的函数关系式(不必写出自变量的取值范围)。16. 如图，有四张质地完全相同的卡片，正面分别写有四个角度，现将这四张卡片洗匀后，背面朝上。
(1)、若从中任意抽取一张，求抽到写有锐角卡片的概率；(2)、若从中任意抽取两张，求抽到的两张卡片写有的角度恰好互补的概率。17. 如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，过D点作AB的垂线交AC于点E。若BC=6，sinA= ，求DE的长。
18. “今有井径五尺，不知其深，立五尺于井上，从木末望水岸，入径2尺，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，请你求出井深BD。
四、解答题(每小题7分，共28分)
-
19. 如图
(1)、图1是4×4的正方形网格，请在其中选取一个白色的正方形涂上阴影，使阴影部分为中心对称图形；(2)、如图2，在正方形网格巾，以点A为旋转中心，将△ABC按逆时针方向旋转90°，画出旋转后的△AB1C1；(3)、如图3，在边长为1个单位长度的小正方形组成的网格中，点A，B，C，O都是格点，作△ABC关于点O的中心对称图形△A1B1C1。20. 某无人机兴趣小组在操场上开展活动(如图)，此时无人机在离地面30米的D处，无人机测得操控者A的俯角为37°，测得点C处的俯角为45°。又经过测量得操控者A和教学楼BC之间的距离为57米，求教学楼BC的高度(注：点A，B，C，D都在同一平面内。结果保留整数。参考数据：sin37°≈0.60，cos37°≈0.80， tan 37°≈0.75)。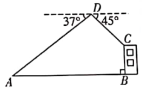
21. 实践操作(1)、如图，△ABC是直角三角形，∠ACB=90°，利用直尺和圆规按下列要求作图，并在图中标明相应的字母(保留作图痕迹，不写作法)。
作∠BAC的平分线，交BC于点O；
(2)、以Ｏ为圆心，OC长为半径作圆。(3)、综合运用在你所作的图中，
AB与⊙O的位置关系是 (直接写出答案)；
(4)、若AC=5，BC=12，求⊙O的半径。22. 某公司种植和销售一种野山菌，已知该野山菌的成本是12元/千克，规定销售价格不低于成本，又不高于成本的两倍．经过市场调查发现，某天该野山菌的销售量y(千克)与销售价格x(元/千克)的函数关系如图所示：
(1)、求y与x之间的函数关系式；(2)、求这一天销售野山菌获得的利润W的最大值。五、解答题(每小题8分，共16分)
-
23. 如图，在平面直角坐标系中，双曲线L：y= (x>0)过点A(a，b)(0<a<2)、B(2，1)。过点A作AC⊥x轴，垂足为C。
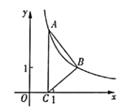(1)、求L的解析式；(2)、当△ABC的面积为2时，求点A的坐标；(3)、点P为双曲线L上A，B之间(包括A，B两点)的动点，直线l1：y=mx+1过点P。在(2)的条件下，若y=mx+1具有y随x的增大而增大的性质，请直接写出m的取值范围(不必说明理由)。24. 小华对图形旋转前后的线段之间、角之间的关系进行了拓展探究。
(1)、(一)猜测探究线在△ABC中，AB=AC，M是平面内任意一点，将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度，得到线段AN，连接NB。
如图1，若Ｍ是线段BC上的任意一点，则∠NAB与∠MAC的数量关系是 ， NB与MC的数量关系是 。
(2)、如图2，点E是AB延长线上一点，若M是∠CBE内部射线BD上任意一点，连接MC，则(1)中结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由。(3)、(二)拓展应用如图3，在△A1B1C1中，A1B1=8，∠A1B1C1=90°，∠C1=30°，点P是B1C1上的任意一点，连接A1P，将A1P绕点A1按顺时针方向旋转60°，得到线段A1Q，连接B1Q。直接写出线段B1Q长度的最小值。
六、解答题(每小题10分，共20分)
-
25. 如图，已知在△ABC中，∠B=90°，AB=8cm，BC=6cm。P，Q是△ABC边上的两个动点，其中点P从点A出发沿A→B方向运动，速度为每秒1cm，到达点B停止运动；点Q从点B出发沿B→C→A方向运动，速度为每秒2cm，到达点A停止运动。它们同时出发，设出发时间为t秒。
(1)、当t=秒时，PQ∥AC；(2)、设△PQB的面积为S，求S关于t的函数关系式，并写出自变量的取值范围；(3)、当点Q在边CA上运动时，直接写出能使△BCQ为等腰三角形的t的值。26. 如图，在平面直角坐标系中，抛物线y=-x²+bx+c与x轴交于A(-1，0)、B两点，与y轴交于点C(0，3)，点Ｐ在该抛物线的对称轴上，且纵坐标为2 。
(1)、求抛物线的表达式以及点Ｐ的坐标；(2)、当三角形中一个内角α是另一个内角β的两倍时，我们称α为此三角形的“特征角”。①当D在射线AP上时，如果∠DAB为∠ABD的特征角，求点D的坐标；
②点E为第一象限内抛物线上一点，点F在x轴上，CE⊥EF，如果∠CEF为△ECF的特征角， 直接写出点E的坐标。