黑龙江省哈尔滨市2020年中考数学一模试卷
试卷更新日期:2020-05-11 类型:中考模拟
一、选择题
-
1. 下列各数中,比-3小的数是( )A、-3 B、-2 C、0 D、-42. 下列计算正确的是( )A、2m+3n=5mn B、(-6x6)+(-2x²)=3x3 C、(3a)-1= D、(x-3)2=x²-93. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
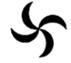 B、
B、 C、
C、 D、
D、 4. 下面的几何体中,主视图为三角形的是( )A、
4. 下面的几何体中,主视图为三角形的是( )A、 B、
B、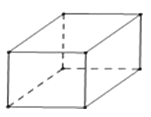 C、
C、 D、
D、 5. 如图,点A是反比例函数y= (x>0)图象上任意一点,AB⊥y轴于点B,点C是x轴上的一个动点,则△ABC的面积为( )
5. 如图,点A是反比例函数y= (x>0)图象上任意一点,AB⊥y轴于点B,点C是x轴上的一个动点,则△ABC的面积为( ) A、1 B、2 C、4 D、无法确定6. 把二次函数y=-x²的图象向左平移1个单位,然后向上平移3个单位,则平移后的图象对应的二次函数的关系式为( )A、y=-(x-1)2-3 B、y=-(x+1)2-3 C、y=-(x-1)2+3 D、y=-(x+1)²+37. 如图,已知∠AOB是⊙O的圆心角,∠AOB=60°,则圆周角∠ACB的度数是( )
A、1 B、2 C、4 D、无法确定6. 把二次函数y=-x²的图象向左平移1个单位,然后向上平移3个单位,则平移后的图象对应的二次函数的关系式为( )A、y=-(x-1)2-3 B、y=-(x+1)2-3 C、y=-(x-1)2+3 D、y=-(x+1)²+37. 如图,已知∠AOB是⊙O的圆心角,∠AOB=60°,则圆周角∠ACB的度数是( ) A、50° B、25° C、100° D、30°8. 如图,把△OAB绕点O逆时针旋转80°,到△OCD的位置,若∠AOB=45°,则∠AOD等于( )
A、50° B、25° C、100° D、30°8. 如图,把△OAB绕点O逆时针旋转80°,到△OCD的位置,若∠AOB=45°,则∠AOD等于( ) A、35° B、90° C、45° D、50°9. 某农场2017年蔬菜产量为50吨,2019年蔬菜产量为60.5吨,该农场蔬菜产量的年平均增长率相同。设该农场蔬菜产量的年平均增长率为x,则根据题意可列方程为( )A、60.5(1-x)2=50 B、50(1-x)2=60.5 C、50(1+x)2=60.5 D、60.5(1+x)²=5010. 如图,在平行四边形ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )
A、35° B、90° C、45° D、50°9. 某农场2017年蔬菜产量为50吨,2019年蔬菜产量为60.5吨,该农场蔬菜产量的年平均增长率相同。设该农场蔬菜产量的年平均增长率为x,则根据题意可列方程为( )A、60.5(1-x)2=50 B、50(1-x)2=60.5 C、50(1+x)2=60.5 D、60.5(1+x)²=5010. 如图,在平行四边形ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:
-
11. 将20 200 000用科学记数法表示为。12. 在函数y= 中,自变量x的取值范围是。13. 化简计算: =。14. 不等式组 的解集为。15. 因式分解:ax²-4ax+4a= 。16. 已知扇形半径是9cm,弧长为4πcm,则扇形的圆心角为度。17. 布袋中装有2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出两个球,摸出的球都是白球的概率是。18. 如图,AB是⊙O的弦,AB=4,C是⊙O上的一个动点,∠ACB=45°,若点M、N分别是AB、BC的中点,则MN长的最大值是。
 19. △ABC中,∠ABC=90°,AC边的垂直平分线交直线BC于点E,若AB=3,BE=4,则tan∠ACB的值为。20. 如图,四边形ABCD中,CD=AD,∠CDA=∠ABD=90°,点E为CD边的中点,连接BE,AB=2,BC= ,则BD=。
19. △ABC中,∠ABC=90°,AC边的垂直平分线交直线BC于点E,若AB=3,BE=4,则tan∠ACB的值为。20. 如图,四边形ABCD中,CD=AD,∠CDA=∠ABD=90°,点E为CD边的中点,连接BE,AB=2,BC= ,则BD=。
三、解答题
-
21. 先化简,再求值 的值,其中x=4sin45°-2cos60°。22. 图1、图2分别是10×8的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的顶点上,请在图1、图2中各取两点C、D(点C、D必须在小正方形的顶点上),使以A、B、C、D为顶点的四边形分别满足以下要求:
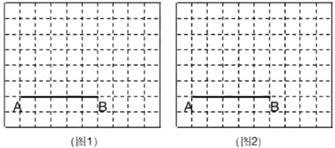 (1)、在图1中画一个菱形ABCD,连接AC,且使tan∠CAB= ;(2)、在图2中画一个以AB为对角线的四边形AEBF,且此四边形为轴对称图形,∠AFB=90°,并直接写出所画四边形的面积;23. 哈市某中学为了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息,回答下列问题:
(1)、在图1中画一个菱形ABCD,连接AC,且使tan∠CAB= ;(2)、在图2中画一个以AB为对角线的四边形AEBF,且此四边形为轴对称图形,∠AFB=90°,并直接写出所画四边形的面积;23. 哈市某中学为了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息,回答下列问题: (1)、本次抽样调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若九年级共有600名学生,请你估计九年级学生中体能测试结果为D等级的学生有多少名?24. 已知平行四边形ABCD,连接AF、CE。AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E,
(1)、本次抽样调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若九年级共有600名学生,请你估计九年级学生中体能测试结果为D等级的学生有多少名?24. 已知平行四边形ABCD,连接AF、CE。AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E, (1)、如图1,求证:四边形AFCE为平行四边形;(2)、如图2,连接BD,分别交AF、CE于G、H,若BC=2AB,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的 的三角形或四边形。25. 电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元、40元。商场销售4台A型号和2台B型号计算器,可获利润80元;销售6台A型号和3台B型号计算器,可获利润120元。(1)、求商场销售A、B两种型号计算器的销售价格分别是多少元?(2)、商场准备用不多于2500元的资金购进A、B两种型号计算器共70台。问最少需要购进A型号的计算器多少台?26. 已知:如图,AB为⊙O的直径,弦CD⊥AB垂足为E,点H为弧AC上一点,连接DH交AB于点F,连接HA、BD,点G为DH上一点,连接AG,∠HAG=∠BDC。
(1)、如图1,求证:四边形AFCE为平行四边形;(2)、如图2,连接BD,分别交AF、CE于G、H,若BC=2AB,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的 的三角形或四边形。25. 电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元、40元。商场销售4台A型号和2台B型号计算器,可获利润80元;销售6台A型号和3台B型号计算器,可获利润120元。(1)、求商场销售A、B两种型号计算器的销售价格分别是多少元?(2)、商场准备用不多于2500元的资金购进A、B两种型号计算器共70台。问最少需要购进A型号的计算器多少台?26. 已知:如图,AB为⊙O的直径,弦CD⊥AB垂足为E,点H为弧AC上一点,连接DH交AB于点F,连接HA、BD,点G为DH上一点,连接AG,∠HAG=∠BDC。 (1)、如图1,求证:AG⊥HD;(2)、如图2,连接HC,若HC=HF,求证:HC=HA;(3)、如图3,连接HO交AG于点K,若点F为DG的中点,HC=2HG,求 的值。27. 已知:如图,在平面直角坐标系中,点O为坐标原点,C(2,0),直线y=2x+6与x轴交于点A,交y轴于点B,过C点作直线AB的垂线,垂足为E,交y轴于点D。
(1)、如图1,求证:AG⊥HD;(2)、如图2,连接HC,若HC=HF,求证:HC=HA;(3)、如图3,连接HO交AG于点K,若点F为DG的中点,HC=2HG,求 的值。27. 已知:如图,在平面直角坐标系中,点O为坐标原点,C(2,0),直线y=2x+6与x轴交于点A,交y轴于点B,过C点作直线AB的垂线,垂足为E,交y轴于点D。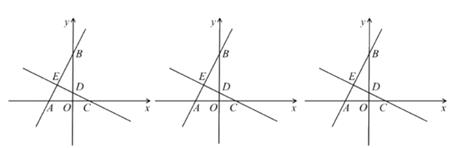 (1)、求直线CD的解析式;(2)、点G为y轴负半轴上一点,连接EG,过点E作EH⊥EG交x轴于点H,设点G的坐标为(0,t),线段AH的长为d,求d与t之间的函数关系式(不要求写出自变量的取值范围)(3)、过点C作x轴的垂线,过点G作y轴的垂线,两线交于点M,过点H作HN⊥GM于点N,交直线CD于点K,连接MK,若MK平分∠NMB,求t的值。
(1)、求直线CD的解析式;(2)、点G为y轴负半轴上一点,连接EG,过点E作EH⊥EG交x轴于点H,设点G的坐标为(0,t),线段AH的长为d,求d与t之间的函数关系式(不要求写出自变量的取值范围)(3)、过点C作x轴的垂线,过点G作y轴的垂线,两线交于点M,过点H作HN⊥GM于点N,交直线CD于点K,连接MK,若MK平分∠NMB,求t的值。