云南省昆明市官渡区2020年学业水平数学一模试卷
试卷更新日期:2020-05-11 类型:中考模拟
一、填空题(每小题3分,满分18分.)
-
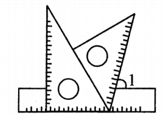
1. 2020的倒数是。2. 使 有意义的x的取值范围为。3. 庚子新春,一场突如其来的新冠肺炎疫情肆虐湖北。举国上下,众志成城,为坚决打赢疫情防控的人民战争、总体战、阻击战,截止2020年2月28日,国家卫健委组织支援湖北的医护人员已超过40000人。数字40000用科学记数法表示为。4. 将一副三角板(含30°、45°、60°、90°角)按如图所示的位置摆放在直尺上,则∠1的。
 5. 若一个多边形的内角和是外角和的3倍,则该多边形的边数是。6. 如图,将半径为6的圆形纸片沿半径OA、OB将其裁成1:3两个部分,用所得扇形围
5. 若一个多边形的内角和是外角和的3倍,则该多边形的边数是。6. 如图,将半径为6的圆形纸片沿半径OA、OB将其裁成1:3两个部分,用所得扇形围成圆锥的侧面,则圆锥的底面半径为。

二、选择题(每小题4分,满分32分.)
-
7. 我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,图乙所示的几何体是形成“牟合方盖”的一种模型,它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 8. 初三(1)班一次体育模拟考试中,10名同学跳绳项目的测试成绩统计如下表:
8. 初三(1)班一次体育模拟考试中,10名同学跳绳项目的测试成绩统计如下表:成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则下列说法错误的是( )
A、平均数是170 B、众数是177 C、中位数是173.5 D、方差是1359. 下列运算中,计算正确的是( )A、a2+a3=a5 B、(3a2)3=27a6 C、a6÷a2=a3 D、(a+b)2=a2+b210. 下列一元二次方程,没有实数根的是( )A、x2-2x-3=0 B、x2-x+1=0 C、x2+2x-3=0 D、x2=111. 不等式组 的解集在数轴上表示正确的是( )A、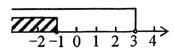 B、
B、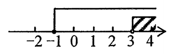 C、
C、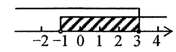 D、
D、 12. 《九章算术》中记录的一道题目译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多1天,如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )A、 B、 C、 D、13. 如图,点A在反比例函数 (x<0)的图象上,点B在反比例函数 (x>0)的图象上,点C在x轴的正半轴上,则平行四边形ABCO的面积是( )
12. 《九章算术》中记录的一道题目译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多1天,如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )A、 B、 C、 D、13. 如图,点A在反比例函数 (x<0)的图象上,点B在反比例函数 (x>0)的图象上,点C在x轴的正半轴上,则平行四边形ABCO的面积是( ) A、6 B、5 C、4 D、314. 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论:
A、6 B、5 C、4 D、314. 如图,在边长为4的正方形ABCD中,E、F是AD边上的两个动点,且AE=FD,连接BE、CF、BD,CF与BD交于点G,连接AG交BE于点H,连接DH,下列结论:①△ABG∽△FDG; ②HD 平分∠EHG;③AG⊥BE;
④S△HDG:S△HBG=tan∠DAG;⑤线段DH的最小值是 .
正确的个数有( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个三、解答题(共9小题,满分70分.)
-
15. 计算:16. 如图,已知∠BAD=∠CAE,AB=AD,AC=AE.求证:∠B=∠D.17. 受非洲猪瘟疫情影响,2019年我国猪肉价格有较大幅度的上升.为了解某地区养殖户的受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行调查(把调查结果分为四个等级:A级—非常严重,B级—严重,C级—般,D级—没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
所抽取养殖户受灾情况统计图
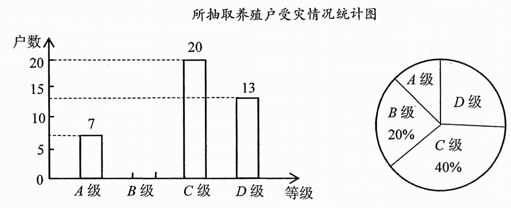 (1)、填空:本次抽样调查的养殖户的总户数是 , 在扇形统计图中A级所对应的圆心角为.(2)、请补全条形统计图;(3)、若该地区建档的养殖户有1500户,估计非常严重与严重的养殖户一共有多少户?18. 近年来,随着互联网经济的兴起和发展,人们的购物模式发生了改变,
(1)、填空:本次抽样调查的养殖户的总户数是 , 在扇形统计图中A级所对应的圆心角为.(2)、请补全条形统计图;(3)、若该地区建档的养殖户有1500户,估计非常严重与严重的养殖户一共有多少户?18. 近年来,随着互联网经济的兴起和发展,人们的购物模式发生了改变,支付方式除了现金支付外,还有微信、支付宝、银行卡等.在一次购物中,小明和小亮都想从微信(记为A)、支付宝(记为B)、银行卡(记为C)三种支付方式中选择一种方式进行支付.
(1)、小明从微信、支付宝、银行卡三种支付方式中选择一种方式进行支付,选择用微信支付的概率为。(2)、请用画树状图或列表的方法,求小明和小亮恰好选择同一种支付方式的概率.19. 在创建全国文明城市过程中,官渡区决定购买A、B两种树苗对某路段道路进行绿化改造.已知购买A种树苗5棵,B种树苗3棵,需要840元;购买A种树苗3棵,B种树苗5棵,需要760元.(1)、求购买A、B两种树苗每棵各需多少元?(2)、现需购进这两种树苗共100棵,考虑到绿化效果和资金周转,购进A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过10000元,怎样购买所需资金最少?20. 阅读材料:若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们称这样的两条抛物线L1、L2互为“友好”抛物线,如图1.
解决问题:如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C.
(1)、若点D与点C关于抛物线L3的对称轴对称,求点D的坐标;(2)、求出以点D为顶点的L3的“友好”抛物线L4的解析式;(3)、直接写出L3与L4中y同时随x增大而增大的自变量x的取值范围.21. 如图,AB为OO的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
 (1)、求证:DE是⊙O的切线.(2)、过点D作DF⊥AB于点F,若BE=33,DF=3,求图中阴影部分的面积.22. 已知,如图1,将△AED绕点E旋转180°得到△BEF,延长FB到点C,使得BC=FB,连接DC.
(1)、求证:DE是⊙O的切线.(2)、过点D作DF⊥AB于点F,若BE=33,DF=3,求图中阴影部分的面积.22. 已知,如图1,将△AED绕点E旋转180°得到△BEF,延长FB到点C,使得BC=FB,连接DC. (1)、求证:四边形ABCD是平行四边形;(2)、如图2,点G是边BC上任意一点(点G与点B、C不重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
(1)、求证:四边形ABCD是平行四边形;(2)、如图2,点G是边BC上任意一点(点G与点B、C不重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.①求证:HC=2AK;
②当点G是BC边中点时,恰有HD=n·HK(n为正整数),求n的值.