上海市闵行区2020年中考数学二模试卷

试卷更新日期：2020-05-11 类型：中考模拟

进入出卷网下载

一、选择题：（本大题共6题，每题4分，满分24分）

1. 在下列各式中，与 $\frac{1}{3} x y^{2}$ 是同类项的是（）

A、 $2 x y$ ； B、 $- y^{2} x$ ； C、 $x y^{2} + \frac{1}{3}$ ； D、 $x^{2} y$ ．

查看试题解析
2. 方程 $x^{2} - 2 \sqrt{3} x + 3 = 0$ 根的情况（）

A、有两个不相等的实数根； B、有一个实数根； C、无实数根； D、有两个相等的实数根．

查看试题解析
3. 在平面直角坐标系中，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 图像在每个象限内，y随着x的增大而增大，那么它的图像的两个分支分别在（）

A、第一、三象限； B、第二、四象限； C、第一、二象限； D、第三、四象限．

查看试题解析
4. 某同学参加射击训练，共发射8发子弹，击中的环数分别为5，3，7，5，6，4，5，5，则下列说法错误的是（）

A、其平均数为5； B、其众数为5； C、其方差为5； D、其中位数为5．

查看试题解析
5. 顺次联结四边形ABCD各边中点所形成的四边形是矩形，那么四边形ABCD是（）

A、平行四边形 B、矩形 C、菱形 D、等腰梯形

查看试题解析
6. 下列命题中正确的个数是（）
① 过三点可以确定一个圆；② 直角三角形的两条直角边长分别是5和12，那么它的外接圆半径为6.5； ③ 如果两个半径为2厘米和3厘米的圆相切，那么圆心距为5厘米；④ 三角形的重心到三角形三边的距离相等．

A、1个； B、2个； C、3个； D、4个．

查看试题解析

二、填空题：（本大题共12题，每题4分，满分48分）

7. 计算： $- 5 + 2^{2} =$ ．

查看试题解析
8. 化简： $\frac{1}{a} - \frac{1}{3 a} =$ ．

查看试题解析
9. 不等式组 ${\begin{cases} 2 (x - 3) > 1 \\ 4 + x > 5 x - 24 \end{cases}$ 的解集是．

查看试题解析
10. 方程 $\sqrt{x - 2} \cdot \sqrt{x - 1} = 0$ 的解是．

查看试题解析
11. 为了考察闵行区1万名九年级学生数学知识与能力测试的成绩，从中抽取50本试卷，每本试卷30份，那么样本容量是．

查看试题解析
12. 如果向量 $\vec{A B}$ 与向量 $\vec{C D}$ 方向相反，且 $| \vec{A B} | = | \vec{C D} | = 5$ ，那么 $\vec{A B} + \vec{C D} =$ ．

查看试题解析
13. 在一张边长为4cm的正方形纸上做扎针随机试验，纸上有一个半径为1cm的圆形阴影区域，那么针头扎在阴影区域内的概率为．（结果保留 $π$ ）

查看试题解析
14. 把直线 $y = - x + b$ 向左平移2个单位后，在y轴上的截距为5，那么原来的直线解析式为．

查看试题解析
15. 已知在梯形ABCD中，AD∥BC ， ∠ABC = 90°，对角线AC、BD相交于点O ，且AC⊥BD ，如果AD︰BC = 2︰3，那么DB︰AC = ．

查看试题解析
16. 七宝琉璃玲珑塔（简称七宝塔），位于上海市七宝古镇的七宝教寺内，塔高47米，共7层．学校老师组织学生利用无人机实地勘测，如果无人机在飞行的某一高度时传回数据，测得塔顶的仰角为60°，塔底的俯角为45°，那么此时无人机距离地面的高度为米．（结果保留根号）

查看试题解析
17. 已知点（ $- 1$ ，y₁），（ $\sqrt{2}$ ，y₂），（2，y₃）在函数 $y = a x^{2} - 2 a x + a - 2$ （ $a > 0$ ）的图像上，那么y₁、y₂、y₃按由小到大的顺序排列是．

查看试题解析
18. 如图，已知在△ABC中，AB=AC=4，∠BAC=30°，将△ABC绕点A顺时针旋转，使点B落在点B₁处，点C落在点C₁处，且BB₁⊥AC ．联结B₁C和C₁C ，那么△B₁C₁C的面积等于．

查看试题解析

三、解答题：（本大题共7题，满分78分）

19. 计算： ${(1 + \sqrt{2})}^{2} - {| - 1 |}^{- 2020} + \frac{1}{2 + \sqrt{3}} - 2^{\frac{3}{2}}$ ．

查看试题解析
20. 解方程组： ${\begin{cases} x - y = 2 ； \\ x^{2} - 2 x y - 3 y^{2} = 0 . \end{cases}$

查看试题解析
21. 已知：如图，在△ABC中，AB=AC=6，BC=4，AB的垂直平分线交AB于点E ，交BC的延长线于点D ．

(1)、求CD的长；

(2)、求点C到ED的距离．

查看试题解析

22. 上海市为了增强居民的节水意识，避免水资源的浪费，全面实施居民“阶梯水价”．当累计水量达到年度阶梯水量分档基数临界点后，即开始实施阶梯价格计价，

分档水量和价格见下表．

分档	户年用水量（立方米）	自来水价格（元/立方米）	污水处理费（元/立方米）
第一阶梯	0-220（含220）	1.92	1.70
第二阶梯	220-300（含300）	3.30	1.70
第三阶梯	300以上	4.30	1.70
注：1．应缴纳水费 = 自来水费总额 + 污水处理费总额 2．应缴纳污水处理费总额 = 用水量×污水处理费× 0.9

仔细阅读上述材料，请解答下面的问题

(1)、小静家2019年上半年共计用水量100立方米，应缴纳水费元；

(2)、小静家全年缴纳的水费共计1000.5元，那么2019年全年用水量为立方米；

(3)、如图所示是上海市“阶梯水价”y与用水量x的函数关系，那么第二阶梯（线段AB）的函数解析式为，定义域．

查看试题解析

23. 如图，已知在□ABCD中，AE⊥BC ，垂足为E ， CE=AB ，点F为CE的中点，点G在线段CD上，联结DF ，交AG于点M ，交EG于点N ，且∠DFC=∠EGC ．

(1)、求证：CG=DG；

(2)、求证： $C G^{2} = G M \cdot A G$ ．

查看试题解析
24. 在平面直角坐标系xOy中，我们把以抛物线 $y = x^{2}$ 上的动点A为顶点的抛物线叫做这条抛物线的“子抛物线”．

如图，已知某条“子抛物线”的二次项系数为 $\frac{3}{2}$ ，且与y轴交于点C ．设点A的横坐标为m（m＞0），过点A作y轴的垂线交y轴于点B ．

(1)、当m=1时，求这条“子抛物线”的解析式；

(2)、用含m的代数式表示∠ACB的余切值；

(3)、如果∠OAC=135°，求m的值．

查看试题解析
25. 如图，已知圆O是正六边形ABCDEF外接圆，直径BE=8，点G、H分别在射线CD、EF上（点G不与点C、D重合），且∠GBH=60°，设CG=x ， EH=y ．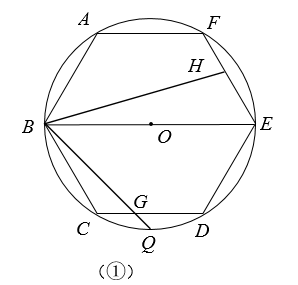

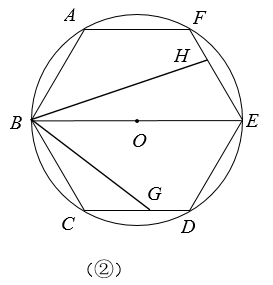
(1)、如图①，当直线BG经过弧CD的中点Q时，求∠CBG的度数；

(2)、如图②，当点G在边CD上时，试写出y关于x的函数关系式，
并写出x的取值范围；

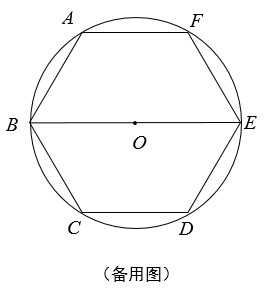
(3)、联结AH、EG ，如果△AFH与△DEG相似，求CG的长．

查看试题解析