2015年湖南省株洲市中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、单选题（每小题3分，共24分）

1. 2的相反数是（　　）

A、-2 B、2 C、- $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 已知∠α=35°，那么∠α的余角等于（　　）

A、35° B、55° C、65° D、145°

查看试题解析
3. 下列等式中，正确的是（　　）

A、3a﹣2a=1 B、a²•a³=a⁵ C、（﹣2a³）²=﹣4a⁶ D、（a﹣b）²=a²﹣b²

查看试题解析
4. 下列几何图形中，既是轴对称图形，又是中心对称图形的是（　　）

A、等腰三角形 B、正三角形 C、平行四边形 D、正方形

查看试题解析
5. 从2，3，4，5中任意选两个数，记作a和b，那么点（a，b）在函数y= $\frac{12}{x}$ 图象上的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6.
如图，圆O是△ABC的外接圆，∠A=68°，则∠OBC的大小是（　　）

A、22° B、26° C、32° D、68°

查看试题解析
7.
如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB=1，CD=3，那么EF的长是（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
8. 有两个一元二次方程M：ax²+bx+c=0；N：cx²+bx+a=0，其中a•c≠0，a≠c．下列四个结论中，错误的是（　　）

A、如果方程M有两个相等的实数根，那么方程N也有两个相等的实数根 B、如果方程M的两根符号相同，那么方程N的两根符号也相同 C、如果5是方程M的一个根，那么 $\frac{1}{5}$ 是方程N的一个根 D、如果方程M和方程N有一个相同的根，那么这个根必是x=1

查看试题解析

二、填空题（每小题3分，共24分）

9. 如果手机通话每分钟收费m元，那么通话n分钟收费元．

查看试题解析
10. 在平面直角坐标系中，点（﹣3，2）关于y轴的对称点的坐标是 .

查看试题解析
11.
如图，l∥m，∠1=120°，∠A=55°，则∠ACB的大小是 .

查看试题解析
12. 某大学自主招生考试只考数学和物理．计算综合得分时，按数学占60%，物理占40%计算．已知孔明数学得分为95分，综合得分为93分，那么孔明物理得分是　分．

查看试题解析
13. 因式分解：x²（x﹣2）﹣16（x﹣2）= .

查看试题解析
14. 已知直线y=2x+（3﹣a）与x轴的交点在A（2，0）、B（3，0）之间（包括A、B两点），则a的取值范围是 .

查看试题解析
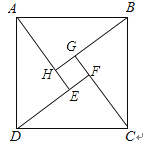
15.
如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=10，EF=2，那么AH等于 .　

查看试题解析
16.
“皮克定理”是用来计算顶点在整点的多边形面积的公式，公式表达式为S=a+ $\frac{b}{2}$ ﹣1，孔明只记得公式中的S表示多边形的面积，a和b中有一个表示多边形边上（含顶点）的整点个数，另一个表示多边形内部的整点个数，但不记得究竟是a还是b表示多边形内部的整点个数，请你选择一些特殊的多边形（如图1）进行验证，得到公式中表示多边形内部的整点个数的字母是，并运用这个公式求得图2中多边形的面积是 .
．

查看试题解析

三、解答题（共7小题，共52分）

17. 计算：|﹣3|+（2015﹣π）⁰﹣2sin30°

查看试题解析
18. 先化简，再求值：（ $\frac{x}{x - 2}$ ﹣ $\frac{3}{x - 2}$ ）• $\frac{x^{2} - 4}{x - 3}$ ，其中x=4．

查看试题解析
19. 为了举行班级晚会，孔明准备去商店购买20个乒乓球做道具，并买一些乒乓球拍做奖品．已知乒乓球每个1.5元，球拍每个22元．如果购买金额不超过200元，且买的球拍尽可能多，那么孔明应该买多少个球拍？

查看试题解析
20.
某学校举行一次体育测试，从所有参加测试的中学生中随机的抽取10名学生的成绩，制作出如下统计表和条形图，请解答下列问题：
编号
成绩
等级
编号
成绩
等级
①
95
A
⑥
76
B
②
78
B
⑦
85
A
③
72
C
⑧
82
B
④
79
B
⑨
77
B
⑤
92
A
⑩
69
C

(1)、孔明同学这次测试的成绩是87分，则他的成绩等级是等；

(2)、请将条形统计图补充完整；

(3)、已知该校所有参加这次测试的学生中，有60名学生成绩是A等，请根据以上抽样结果，估计该校参加这次测试的学生总人数是多少人．

查看试题解析
21. P表示n边形对角线的交点个数（指落在其内部的交点），如果这些交点都不重合，那么P与n的关系式是P= $\frac{n (n - 1)}{24}$ （n²﹣an+b）（其中a，b是常数，n≥4）

(1)、
填空：通过画图可得：

四边形时，P=（填数字）；五边形时，P=（填数字）

(2)、请根据四边形和五边形对角线的交点个数，结合关系式，求a和b的值．（注：本题中的多边形均指凸多边形）

查看试题解析
22.
如图，在Rt△ABC中，∠C=90°，BD是△ABC的一条角平分线．点O、E、F分别在BD、BC、AC上，且四边形OECF是正方形．

(1)、求证：点O在∠BAC的平分线上；

(2)、若AC=5，BC=12，求OE的长．

查看试题解析
23.
已知AB是圆O的切线，切点为B，直线AO交圆O于C、D两点，CD=2，∠DAB=30°，动点P在直线AB上运动，PC交圆O于另一点Q．

(1)、当点P运动到使Q、C两点重合时（如图1），求AP的长；

(2)、点P在运动过程中，有几个位置（几种情况）使△CQD的面积为 $\frac{1}{2}$ ？（直接写出答案）

(3)、当△CQD的面积为 $\frac{1}{2}$ ，且Q位于以CD为直径的上半圆，CQ＞QD时（如图2），求AP的长．

查看试题解析

编号	成绩	等级	编号	成绩	等级
①	95	A	⑥	76	B
②	78	B	⑦	85	A
③	72	C	⑧	82	B
④	79	B	⑨	77	B
⑤	92	A	⑩	69	C

2015年湖南省株洲市​中考数学真题试卷

一、单选题（每小题3分，共24分）

二、填空题（每小题3分，共24分）

三、解答题（共7小题，共52分）

2015年湖南省株洲市中考数学真题试卷