2015年湖南省湘西州中考数学真题试卷

试卷更新日期：2016-04-25 类型：中考真卷

进入出卷网下载

一、填空题

1. ﹣2015的绝对值是 .

查看试题解析
2.
如图，直线a，b被直线c所截，且a∥b，∠1=40°，则∠2=度．

查看试题解析
3. 分解因式：x²﹣4= .

查看试题解析
4. 每年的5月31日为世界无烟日，开展无烟日活动旨在提醒世人吸烟有害健康，呼吁全世界吸烟者主动放弃吸烟，全世界每年因吸烟而引发疾病死亡的人数大约为5400000人，数据5400000人用科学记数法表示为 .

查看试题解析
5. 掷一枚质地均匀的骰子，六个面上分别标有1，2，3，4，5，6；则出现点数为1的概率为 .

查看试题解析
6. 要使分式 $\frac{1}{2 - x}$ 有意义，则x的取值范围是 .

查看试题解析
7.
如图，在△ABC中，E，F分别为AB，AC的中点，则△AEF与△ABC的面积之比为 .

查看试题解析
8.
如图，在⊙O中，∠OAB=45°，圆心O到弦AB的距离OE=2cm，则弦AB的长为 cm．

查看试题解析

二、选择题（本大题共10小题，每小题4分，共40分）

9. 下列运算正确的是（　　）

A、a+2a=2a² B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、（x﹣3）²=x²﹣9 D、（x²）³=x⁶

查看试题解析
10. 在平面直角坐标系中，点A（﹣2，1）与点B关于原点对称，则点B的坐标为（　　）

A、（﹣2，1） B、（2，﹣1） C、（2，1） D、（﹣2，﹣1）

查看试题解析
11. 下列几何体中，主视图、左视图、俯视图完全相同的是（　　）

A、球 B、圆锥 C、圆柱 D、长方体

查看试题解析
12. 湘西土家族苗族自治州6月2日至6月8日最高气温（℃）统计如下表：
日期
2日
3日
4日
5日
6日
7日
8日
最高气温℃
28
25
25
30
32
28
27
则这七天最高气温的中位数为（　　）

A、25℃ B、27℃ C、28℃ D、30℃

查看试题解析
13. 下列方程中，没有实数根的是（　　）

A、x²﹣4x+4=0 B、x²﹣2x+5=0 C、x²﹣2x=0 D、x²﹣2x﹣3=0

查看试题解析
14. 式子2 $\sqrt{3}$ + $\sqrt{2}$ 的结果精确到0.01为（可用计算器计算或笔算）（　　）

A、4.9 B、4.87 C、4.88 D、4.89

查看试题解析
15. ⊙O的半径为5cm，点A到圆心O的距离OA=3cm，则点A与圆O的位置关系为（　　）

A、点A在圆上 B、点A在圆内 C、点A在圆外 D、无法确定

查看试题解析
16.
如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠1的度数为（　　）

A、36° B、60° C、72° D、108°

查看试题解析
17. 已知k＞0，b＜0，则一次函数y=kx﹣b的大致图象为（　　）

A、 B、 C、 D、

查看试题解析
18. 下列说法中，正确的是（　　）

A、三点确定一个圆 B、一组对边平行，另一组对边相等的四边形是平行四边形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分且相等的四边形是正方形

查看试题解析

三、解答题：本大题共8小题，共78分

19. 计算：3²﹣2015⁰+tan45°．

查看试题解析
20.
解不等式组 $\{\begin{matrix} x - 2 \leq 1 \\ 2 x + 3 \geq 1 \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
21.
如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F．

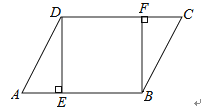(1)、求证：△ADE≌△CBF；

(2)、求证：四边形BFDE为矩形．

查看试题解析
22.
如图，已知反比例函数y= $\frac{k}{x}$ 的图象经过点A（﹣3，﹣2）．

(1)、求反比例函数的解析式；

(2)、若点B（1，m），C（3，n）在该函数的图象上，试比较m与n的大小．

查看试题解析
23. 某教研机构为了了解初中生课外阅读名著的现状，随机抽取了某校50名初中生进行调查，依据相关数据绘制成了以下不完整的统计图，请根据图中信息解答下列问题：
类别
重视
一般
不重视
人数
a
15
b

(1)、求表格中a，b的值；

(2)、
请补全统计图；

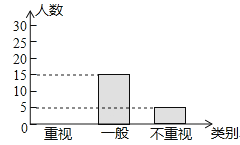(3)、若某校共有初中生2000名，请估计该校“重视课外阅读名著”的初中生人数．

查看试题解析
24. 湘西自治州风景优美，物产丰富，一外地游客到某特产专营店，准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产．若购买3盒豆腐乳和2盒猕猴桃果汁共需180元；购买1盒豆腐乳和3盒猕猴桃果汁共需165元．

(1)、请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格；

(2)、该游客购买了4盒豆腐乳和2盒猕猴桃果汁，共需多少元？

查看试题解析
25.
如图，台风中心位于点O处，并沿东北方向（北偏东45°），以40千米/小时的速度匀速移动，在距离台风中心50千米的区域内会受到台风的影响，在点O的正东方向，距离 $60 \sqrt{2}$ 千米的地方有一城市A．

(1)、问：A市是否会受到此台风的影响，为什么？

(2)、在点O的北偏东15°方向，距离80千米的地方还有一城市B，问：B市是否会受到此台风的影响？若受到影响，请求出受到影响的时间；若不受到影响，请说明理由．

查看试题解析
26.
如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线y=﹣x²+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以 $\sqrt{2}$ 个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．

(1)、求抛物线的解析式；

(2)、问：当t为何值时，△APQ为直角三角形；

(3)、过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标.

(4)、设抛物线顶点为M，连接BP，BM，MQ，问：是否存在t的值，使以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析

日期	2日	3日	4日	5日	6日	7日	8日
最高气温℃	28	25	25	30	32	28	27

类别	重视	一般	不重视
人数	a	15	b