湖南省株洲市石峰区2019年中考数学模拟试卷（二)

试卷更新日期：2020-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\sqrt{2}$ 的绝对值是（　　）

A、 $\sqrt{2}$ B、﹣ $\sqrt{2}$ C、2 D、﹣2

查看试题解析
2. 下列计算正确的是（）

A、a⁴+a³＝a⁷ B、a⁴•a³＝a¹² C、（a⁴）³＝a⁷ D、a⁴÷a³＝a

查看试题解析
3. 生物学家发现了某种花粉的直径约为0.0000036毫米，数据0.0000036用科学记数法表示正确的是（）

A、3.6×10^﹣5 B、0.36×10^﹣5 C、3.6×10^﹣6 D、0.36×10^﹣6

查看试题解析
4. 数据1，2，3，4，4，5的众数和中位数的差是（）

A、1 B、﹣0.5 C、0.5 D、﹣1

查看试题解析
5. 下列图形中，既是轴对称又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 不等式组 ${\begin{array}{l} 2 x > - x \\ x - 1 > 4 (x - 1) \end{array}$ 的解集为（）

A、x＞0 B、x＞1 C、无解 D、0＜x＜1

查看试题解析
7. 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结 $OE .$ 若 $∠ ABC = 60^{\circ}$ ， $∠ BAC = 80^{\circ}$ ，则 $∠ 1$ 的度数为（）

A、 $50^{\circ}$ B、 $40^{\circ}$ C、 $30^{\circ}$ D、 $20^{\circ}$

查看试题解析
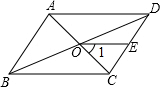8. 当x＞0时，y随x的增大而增大的函数是（）

A、y＝﹣x B、y＝ $\frac{1}{x}$ C、y＝－ $\frac{1}{x}$ D、y＝﹣x²

查看试题解析
9. 如图，已知点E是矩形ABCD的对角线AC上的一动点，正方形EFGH的顶点G、H都在边AD上，若AB=3，BC=4，则tan∠AFE的值（）

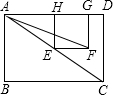A、等于 $\frac{3}{7}$ B、等于 $\frac{\sqrt{3}}{3}$ C、等于 $\frac{3}{4}$ D、随点E位置的变化而变化

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于点A（-1，0），顶点坐标（1，n）与 $y$ 轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：① $3 a + b < 0$ ；② $- 1 \leq a \leq - \frac{2}{3}$ ；③对于任意实数m，a+b≥am²+bm总成立；④关于 $x$ 的方程 $a x^{2} + b x + c = n - 1$ 有两个不相等的实数根.其中结论正确的个数为 $($ 　　 $)$

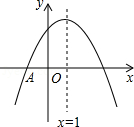A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析

二、填空题

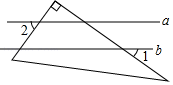
11. 分式方程 $\frac{1}{x} = \frac{2}{x - 1}$ 的解是．

查看试题解析
12. 已知a∥b ，某学生将一直角三角板放置如图所示，如果∠1＝35°，则∠2的度数为．

查看试题解析
13. 因式分解：x³﹣4x²+4x＝．

查看试题解析
14. 一个三角形的两边长分别为3和6，第三边长是方程x²-10x+21=0的根，则三角形的周长为.

查看试题解析
15. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题，译文为：“现有几个人共同购买一个物品，每人出8元，则多3元；每人出7元，则差4元．问这个物品的价格是多少元？”该物品的价格是元．

查看试题解析
16. 如图，正六边形ABCDEF外接圆的半径为4，则其内切圆的半径是．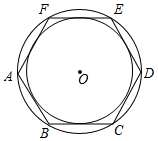

查看试题解析
17. 如图，平行于x轴的直线与函数y＝ $\frac{k_{1}}{x}$ （k₁＞0，x＞0），y＝ $\frac{k_{2}}{x}$ （k₂＞0，x＞0）的图象分别相交于A ， B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为3，则k₁﹣k₂的值为．

查看试题解析
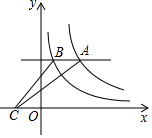18. 如图，往竖直放置的在A处山短软管连接的粗细均匀细管组成的“U形装置中注入一定量的水，水面高度为9cm ，现将右边细管绕A处顺时针方向旋转60°到AB位置，则AB中水柱的长度为cm ．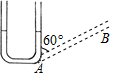

查看试题解析

三、综合题

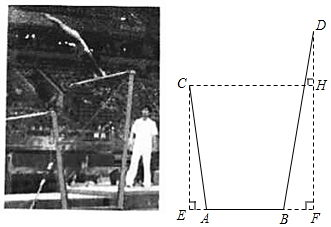
19. 计算： $\sqrt{\frac{1}{2}} \times \sqrt{6} + \sqrt[3]{8} - \tan 60^{0} + {(\frac{1}{2})}^{- 2}$

查看试题解析
20. 先化简，再求值：（x﹣1+ $\frac{2 - 2 x}{x + 1}$ ）÷ $\frac{x^{2} - x}{x + 1}$ ，其中x的值从不等式﹣1≤x＜2.5的整数解中选取．

查看试题解析
21. “高低杠”是女子体操特有的一个竞技项目，其比赛器材由高、低两根平行杠及若干支架组成，运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离．某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题，请你解答．
如图所示，底座上A，B两点间的距离为90cm．低杠上点C到直线AB的距离CE的长为155cm，高杠上点D到直线AB的距离DF的长为234cm，已知低杠的支架AC与直线AB的夹角∠CAE为82.4°，高杠的支架BD与直线AB的夹角∠DBF为80.3°．求高、低杠间的水平距离CH的长．（结果精确到1cm，参考数据sin82.4°≈0.991，cos82.4°≈0.132，tan82.4°≈7.500，sin80.3°≈0.983，cos80.3°≈0.168，tan80.3°≈5.850）

查看试题解析
22. 央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题：
图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”.

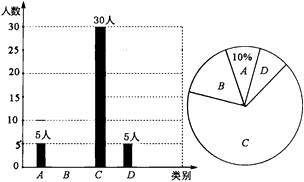(1)、被调查的总人数是人，扇形统计图中C部分所对应的扇形圆心角的度数为.

(2)、补全条形统计图；

(3)、若该校共有学生1800人，请根据上述调查结果，估计该校学生中A类有人；

(4)、在抽取的A类5人中，刚好有3个女生2个男生，从中随机抽取两个同学担任两角色，用树形图或列表法求出被抽到的两个学生性别相同的概率.

查看试题解析
23. 如图，四边形ABCD是矩形，E是BD上的一点，∠BAE＝∠BCE，∠AED＝∠CED，点G是BC，AE延长线的交点，AG与CD相交于点F．

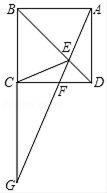(1)、求证：四边形ABCD是正方形；

(2)、当AE＝3EF，DF＝1时，求GF的值．

查看试题解析
24. 如图，一次函数y₁＝kx+b（k ， b为常数，k≠0）的图象与反比例函数y₂＝ $\frac{m}{x}$ （m为常数，m≠0）的图象相交于点M（1，4）和点N（4，n）．

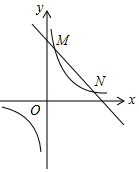(1)、反比例函数与一次函数的解析式．

(2)、函数y₂＝ $\frac{m}{x}$ 的图象（x＞0）上有一个动点C ，若先将直线MN平移使它过点C ，再绕点C旋转得到直线PQ ， PQ交x轴于点A ，交y轴点B ，若BC＝2CA ，求OA•OB的值．

查看试题解析
25. 如图，已知AB是⊙O的直径，AC是弦（不是直径），OD⊥AC垂足为G交⊙O于D ， E为⊙O上一点（异于A、B），连接ED交AC于点F ，过点E的直线交BA、CA的延长线分别于点P、M ，且ME＝MF ．

(1)、求证：PE是⊙O的切线．

(2)、若DF＝2，EF＝8，求AD的长．

(3)、若PE＝6 $\sqrt{2}$ ，sin∠P＝ $\frac{1}{3}$ ，求AE的长．

查看试题解析
26. 已知二次函数y＝x²+bx+c+1的图象与x轴交于点A（x₁ ， 0）、B（x₂ ， 0），且x₁＜x₂ ，与y轴的负半轴交于点C ．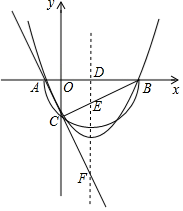

(1)、当b＝1时，求c的取值范围；

(2)、如果以AB为直径的半圆恰好过点C ，求c的值；

(3)、在（2）的条件下，如果二次函数的对称轴l与x轴、直线BC、直线AC的延长线分别交于点D、E、F ，且满足DE＝2EF ，求二次函数的表达式．

查看试题解析