湖南省株洲市石峰区2019年中考数学模拟试卷(一)
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. ﹣3的相反数是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 学校准备从甲、乙、丙、丁四个科技创新小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差 如表所示:
甲
乙
丙
丁
7
8
8
7
1
1.2
1
1.8
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
A、甲 B、乙 C、丙 D、丁4. 左下图是由六个相同的小立方块搭成的几何体,这个几何体的俯视图是( ) A、
A、 B、
B、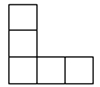 C、
C、 D、
D、 5. 点A(﹣1,1)是反比例函数y=的图象上一点,则m的值为( )A、﹣1 B、﹣2 C、0 D、16. 不等式组 的解集在数轴上表示正确的是( )A、
5. 点A(﹣1,1)是反比例函数y=的图象上一点,则m的值为( )A、﹣1 B、﹣2 C、0 D、16. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
7. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )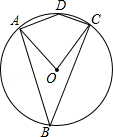 A、80° B、100° C、60° D、40°8. 如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( )
A、80° B、100° C、60° D、40°8. 如图,在四边形ABCD中,E、F分别是AB、AD中点,若EF=2,BC=5,CD=3,则tanC等于( ) A、 B、 C、 D、9. 从-2、-1、0、1、2这5个数中任取一个数,作为关于x的一元二次方程x2-2x+k=0的k值,则所得的方程中有两个不相等的实数根的概率是( )A、 B、 C、 D、10. 已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点.现有以下四个结论:①该抛物线的对称轴一定在y轴的左侧;②a-b+c≥0;③关于x的方程ax2+bx+c=2一定无实数根;④ 的最小值是3,其中正确结论的个数是( )A、1 B、2 C、3 D、4
A、 B、 C、 D、9. 从-2、-1、0、1、2这5个数中任取一个数,作为关于x的一元二次方程x2-2x+k=0的k值,则所得的方程中有两个不相等的实数根的概率是( )A、 B、 C、 D、10. 已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点.现有以下四个结论:①该抛物线的对称轴一定在y轴的左侧;②a-b+c≥0;③关于x的方程ax2+bx+c=2一定无实数根;④ 的最小值是3,其中正确结论的个数是( )A、1 B、2 C、3 D、4二、填空题
-
11. 多项式1+x+2xy-3xy2的次数是 .12. 因式分解:x3-25x .13. 函数 的自变量x的取值范围是 .14. 菱形的两条对角线的长是方程x2-7x+1=0的两根,则菱形的面积是 .15. 如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C=度.
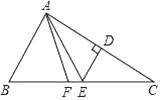 16. 若关于x的分式方程 =2的解为正实数,则整数m的最大值是 .17. 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=8cm,EF=15cm,则边AD的长是cm.
16. 若关于x的分式方程 =2的解为正实数,则整数m的最大值是 .17. 如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=8cm,EF=15cm,则边AD的长是cm. 18. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(-3,0),且两直线与y轴围成的三角形面积为15,那么b1-b2等于 .
18. 直线y=k1x+b1(k1>0)与y=k2x+b2(k2<0)相交于点(-3,0),且两直线与y轴围成的三角形面积为15,那么b1-b2等于 .三、综合题
-
19. 先化简,再求值:(1 )÷ ,其中x是从0,1,2,3中选取的一个合适的数.20. 计算:4cos30°21. 如图,小明在M处用高1.5米(DM=1.5米)的测角仪测得学校旗杆AB的顶端B的仰角为32°,再向旗杆方向前进9米到F处,又测得旗杆顶端B的仰角为64°,请求出旗杆AB的高度(sin64°≈0.9,cos64°≈0.4,tan64°≈2.1,结果保留整数).
 22. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分.
22. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分.分组
家庭用水量x/吨
家庭数/户
A
0≤x≤4.0
4
B
4.0<x≤6.5
13
C
6.5<x≤9.0
D
9.0<x≤11.5
E
11.5<x≤14.0
6
F
x>14.0
3

根据以上信息,解答下列问题:
(1)、本次抽样调查的家庭数为户.(2)、家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是;(3)、家庭用水量的中位数在组.(4)、若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.23. 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M. (1)、求证:△ABF≌△CBN;(2)、求 的值.24. 如图,在平面直角坐标系中,四边形OABC是矩形,且B(6,4),F是AB上的一个动点(F不与A,B重合),过点的反比例函数y= (k>0)的图象与BC边交于点E,连接AE.
(1)、求证:△ABF≌△CBN;(2)、求 的值.24. 如图,在平面直角坐标系中,四边形OABC是矩形,且B(6,4),F是AB上的一个动点(F不与A,B重合),过点的反比例函数y= (k>0)的图象与BC边交于点E,连接AE. (1)、当F为AB的中点时,求反比例函数和直线AE的解析式.(2)、设△EFA的面积为S,当k为何值时,S最大?并求出这个最大值.
(1)、当F为AB的中点时,求反比例函数和直线AE的解析式.(2)、设△EFA的面积为S,当k为何值时,S最大?并求出这个最大值.

