湖南省永州市双牌县2019年中考数学一模试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. ﹣ 的倒数的相反数等于( )A、﹣2 B、 C、﹣ D、22. 某市今年约有140000人报名参加初中学业水平考试,用科学记数法表示140000为( )A、14×104 B、14×103 C、1.4×104 D、1.4×1053. 在下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 直角三角形
B、
直角三角形
B、 正五边形
C、
正五边形
C、 正方形
D、
正方形
D、 平行四边形
4. 下列运算正确的是( )A、 B、 C、 D、5.
平行四边形
4. 下列运算正确的是( )A、 B、 C、 D、5.一个几何体的三视图如图所示,则这个几何体是( )
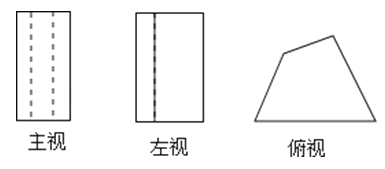 A、
A、 B、
B、 C、
C、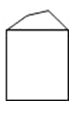 D、
D、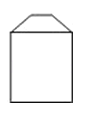 6. 小明把一副 的直角三角板如图摆放,其中 ,则 等于( )
6. 小明把一副 的直角三角板如图摆放,其中 ,则 等于( ) A、 B、 C、 D、7. 从1、2、3三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为( )A、 B、 C、 D、8. △ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.如图,若 的长为12cm,那么 的长是( )
A、 B、 C、 D、7. 从1、2、3三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为( )A、 B、 C、 D、8. △ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.如图,若 的长为12cm,那么 的长是( ) A、10cm B、9cm C、8cm D、6cm9. 函数y1=|x|, .当y1>y2时,x的范围是( )
A、10cm B、9cm C、8cm D、6cm9. 函数y1=|x|, .当y1>y2时,x的范围是( ) A、 B、 C、 或 D、10. 在平面直角坐标系中,将抛物线y=x2-4先向右平移两个单位,再向上平移两个单位,得到的抛物线的解析式是( )A、 B、 C、 D、
A、 B、 C、 或 D、10. 在平面直角坐标系中,将抛物线y=x2-4先向右平移两个单位,再向上平移两个单位,得到的抛物线的解析式是( )A、 B、 C、 D、二、填空题
-
11. 分解因式:a3-12a2+36a= .12. 分式方程 - =0的解为 .13. 在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 , 众数是 .14. 如图,在平面直角坐标系中,点A的坐标为(-1, ),以原点O为中心,将点A顺时针旋转90°得到点A′,则点A′坐标为 .
 15. 已知等腰三角形的腰与底边的长分别是一元二次方程x2-6x+8=0的解,则该三角形的面积是 .16. 如图,在△ABC中,∠B与∠C的平分线交于点O. 过O点作DE∥BC,分别交AB、AC于D、E.若AB=5,AC=4,则△ADE的周长是.
15. 已知等腰三角形的腰与底边的长分别是一元二次方程x2-6x+8=0的解,则该三角形的面积是 .16. 如图,在△ABC中,∠B与∠C的平分线交于点O. 过O点作DE∥BC,分别交AB、AC于D、E.若AB=5,AC=4,则△ADE的周长是.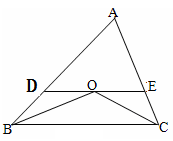 17. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…用你所发现的规律得出22019的末位数字是.18. 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ﹣1;以上结论中正确结论的序号为 .
17. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…用你所发现的规律得出22019的末位数字是.18. 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ﹣1;以上结论中正确结论的序号为 .
三、综合题
-
19. 为推进郴州市创建国家森林城市工作,尽快实现“让森林走进城市,让城市拥抱森林”的构想,今年三月份,某县园林办购买了甲、乙两种树苗共1000棵,其中甲种树苗每棵40元,乙种树苗每棵50元,据相关资料表明:甲、乙两种树苗的成活率分别为85%和90%.(1)、若购买甲、乙两种树苗共用去了46500元,则购买甲、乙两种树苗各多少棵?(2)、若要使这批树苗的成活率不低于88%,则至多可购买甲种树苗多少棵?20. 计算:2sin30°+(π-3.14)0+|1- |+( )-1+(-1)201921. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴交于A、B两点,交反比例函数于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,-1),DE=3.
 (1)、求反比例函数与一次函数的解析式(2)、根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值.(3)、求△OAD的面积S△OAD .22. 先化简(1- )÷ ,再从不等式2x-1<6的正整数解中选一个适当的数代入求值.23. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.
(1)、求反比例函数与一次函数的解析式(2)、根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值.(3)、求△OAD的面积S△OAD .22. 先化简(1- )÷ ,再从不等式2x-1<6的正整数解中选一个适当的数代入求值.23. 为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表.组别
分数段
频次
频率
A
60≤x<70
17
0.17
B
70≤x<80
30
a
C
80≤x<90
b
0.45
D
90≤x<100
8
0.08
请根据所给信息,解答以下问题:
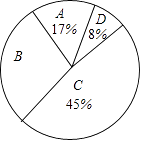 (1)、表中a= , b=;(2)、请计算扇形统计图中B组对应扇形的圆心角的度数;(3)、已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.24. 如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)、表中a= , b=;(2)、请计算扇形统计图中B组对应扇形的圆心角的度数;(3)、已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率.24. 如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.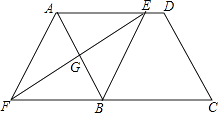 (1)、求证:△AGE≌△BGF;(2)、试判断四边形AFBE的形状,并说明理由.25. 在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB、AC相交于点D、E,过点D作DF⊥AC,垂足为点F.
(1)、求证:△AGE≌△BGF;(2)、试判断四边形AFBE的形状,并说明理由.25. 在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB、AC相交于点D、E,过点D作DF⊥AC,垂足为点F. (1)、求证:DF是⊙O的切线;(2)、分别延长CB、FD相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.26. 如图,已知抛物线y=ax2+ x+c与x轴交于A,B两点,与y轴交于C点,且A(2,0),C(0,-4),直线l:y=- x-4与x轴交于点D,点P是抛物线y=ax2+ x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于F.
(1)、求证:DF是⊙O的切线;(2)、分别延长CB、FD相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.26. 如图,已知抛物线y=ax2+ x+c与x轴交于A,B两点,与y轴交于C点,且A(2,0),C(0,-4),直线l:y=- x-4与x轴交于点D,点P是抛物线y=ax2+ x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于F. (1)、试求该抛物线表达式;(2)、如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;(3)、如图(2),连接AC.求证:△ACD是直角三角形.27. 如图所示,
(1)、试求该抛物线表达式;(2)、如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;(3)、如图(2),连接AC.求证:△ACD是直角三角形.27. 如图所示, (1)、正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;(2)、将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;(3)、将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=a,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用a表示出直线BE、DF形成的锐角β.
(1)、正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;(2)、将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;(3)、将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=a,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用a表示出直线BE、DF形成的锐角β.