湖南省邵阳市新宁县2019年中考数学一模试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. 对 描述不正确的一项是( )A、面积为2的正方形的边长 B、它是一个无限不循环小数 C、它是2的一个平方根 D、它的小数部分大于2-2. 下列调查中,适合进行普查的是( )A、一个班级学生的体重 B、我国中学生喜欢上数学课的人数 C、一批灯泡的使用寿命 D、《新闻联播》电视栏目的收视率3. 下列图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、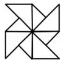 C、
C、 D、
D、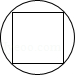 4. 一次函数y=kx+b经过第一、三、四象限,则下列正确的是( )A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<05. 将一条两边沿平行的纸带如图折叠,若∠1=62°,则∠2等于( )
4. 一次函数y=kx+b经过第一、三、四象限,则下列正确的是( )A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<05. 将一条两边沿平行的纸带如图折叠,若∠1=62°,则∠2等于( )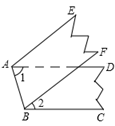 A、62° B、56° C、45° D、30°6. 如图,直线a∥b,∠1=72°,则∠2的度数是( )
A、62° B、56° C、45° D、30°6. 如图,直线a∥b,∠1=72°,则∠2的度数是( ) A、118° B、108° C、98° D、72°7. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A、118° B、108° C、98° D、72°7. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )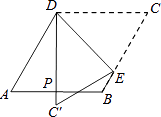 A、78° B、75° C、60° D、45°8. 若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2 , 且x1≠x2 , 有下列结论:
A、78° B、75° C、60° D、45°8. 若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2 , 且x1≠x2 , 有下列结论:①x1=2,x2=3; ② ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,符合题意结论的个数是( )
A、0 B、1 C、2 D、39. 2022年将在北京﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛,为此对这两名队员进行了五次测试,测试成绩如图所示:则下列说法中正确的是( ) A、SA2>SB2 , 应该选取B选手参加比赛 B、SA2<SB2 , 应该选取A选手参加比赛 C、SA2≥SB2 , 应该选取B选手参加比赛 D、SA2≤SB2 , 应该选取A选手参加比赛10. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则cos∠CBE的值是( )
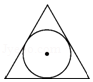
A、SA2>SB2 , 应该选取B选手参加比赛 B、SA2<SB2 , 应该选取A选手参加比赛 C、SA2≥SB2 , 应该选取B选手参加比赛 D、SA2≤SB2 , 应该选取A选手参加比赛10. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则cos∠CBE的值是( ) A、 B、 C、 D、11. 如图, 是一块绿化带,将阴影部分修建为花圃.已知 , , ,阴影部分是 的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( ).
A、 B、 C、 D、11. 如图, 是一块绿化带,将阴影部分修建为花圃.已知 , , ,阴影部分是 的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( ).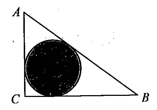 A、 B、 C、 D、12. 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
A、 B、 C、 D、12. 如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )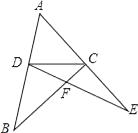 A、114° B、123° C、132° D、147°
A、114° B、123° C、132° D、147°二、填空题
-
13. ﹣ 的倒数是 .14. 写出一个二次项系数为1,且一个根是3的一元二次方程 .
15. 若关于x的不等式3m﹣2x<5的解集是x>3,则实数m的值为 .16. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF2为 .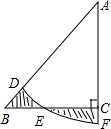 17. 如图,△ABC中,AB=AC,∠A=40º,点P是△ABC内一点,连结PB、PC,∠1=∠2,则∠BPC的度数是.
17. 如图,△ABC中,AB=AC,∠A=40º,点P是△ABC内一点,连结PB、PC,∠1=∠2,则∠BPC的度数是.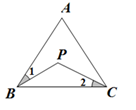 18. 若如图中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到如图称第1次操作,再将如图中的每一段类似变形,得到如图即第2次操作,按上述方法继续得到如图为第3次操作,则第4次操作后折线的总长度为 .
18. 若如图中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到如图称第1次操作,再将如图中的每一段类似变形,得到如图即第2次操作,按上述方法继续得到如图为第3次操作,则第4次操作后折线的总长度为 . 19. 如图,在平面直角坐标系中,将点P(-4,2)绕原点顺时针旋转90°,求其对应点Q的坐标.
19. 如图,在平面直角坐标系中,将点P(-4,2)绕原点顺时针旋转90°,求其对应点Q的坐标. 20. 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 .
20. 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 .
三、综合题
-
21. 计算:(1)、(2)、22. 解方程: .23. 如果x2+Ax+B=(x﹣3)(x+5),求3A﹣B的值.24. 已知如图在△ABC 中,∠ABC平分线与∠ACE的外角平分线相交于点P.若∠A=70°,求∠P的度数.
 25. 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ,求旗杆AB的高度( ≈1.73,结果精确到个位).
25. 如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ,求旗杆AB的高度( ≈1.73,结果精确到个位). 26. 如图已知直线AC的函数解析式为y= x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?
26. 如图已知直线AC的函数解析式为y= x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?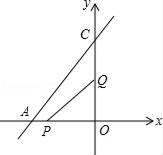 27. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.(1)、求该种水果每次降价的百分率;(2)、从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
27. 某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.(1)、求该种水果每次降价的百分率;(2)、从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?时间x(天)
1≤x<9
9≤x<15
x≥15
售价(元/斤)
第1次降价后的价格
第2次降价后的价格
销量(斤)
80﹣3x
120﹣x
储存和损耗费用(元)
40+3x
3x2﹣64x+400
(3)、在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?28. 在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC= ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直. (1)、如图1,当点R与点D重合时,求PQ的长;(2)、如图2,试探索: 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)、如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.
(1)、如图1,当点R与点D重合时,求PQ的长;(2)、如图2,试探索: 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)、如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.