湖南省邵阳市邵阳县2019年中考数学二模试卷
试卷更新日期:2020-05-09 类型:中考模拟
一、选择题
-
1. 下列无理数中,与 最接近的是( )A、 B、 C、 D、2. 如图所示,直线AB , CD相交于点O , OE⊥CD , 已知∠BOE=65°,则∠AOC的大小为( )
 A、25° B、35° C、65° D、115°3. 下列运算正确的是( )A、3a2﹣2a2=1 B、(﹣a2b3)2=a4b6 C、(﹣a2)3=﹣a5 D、a2•a3=a64. 下列立体图形中,主视图是圆的是( )A、
A、25° B、35° C、65° D、115°3. 下列运算正确的是( )A、3a2﹣2a2=1 B、(﹣a2b3)2=a4b6 C、(﹣a2)3=﹣a5 D、a2•a3=a64. 下列立体图形中,主视图是圆的是( )A、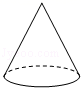 B、
B、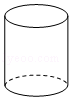 C、
C、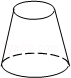 D、
D、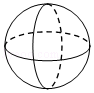 5. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<06. 如图,已知圆心角∠AOB=110°,则圆周角∠ACB=( )
5. 已知x1、x2是关于x的方程x2﹣ax﹣2=0的两根,下列结论一定正确的是( )A、x1≠x2 B、x1+x2>0 C、x1•x2>0 D、x1<0,x2<06. 如图,已知圆心角∠AOB=110°,则圆周角∠ACB=( )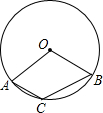 A、55° B、110° C、120° D、125°7. “五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
A、55° B、110° C、120° D、125°7. “五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”区域的次数m
68
108
140
355
560
690
落在“铅笔”区域的频率
0.68
0.72
0.70
0.71
0.70
0.69
下列说法不正确的是( )
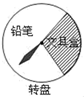 A、当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70 B、假如你去转动转盘一次,获得“铅笔”概率大约是0.70 C、如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次 D、转动转盘20次,一定有6次获得“文具盒”8. 某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图,由图可知,下列结论正确的是( )
A、当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70 B、假如你去转动转盘一次,获得“铅笔”概率大约是0.70 C、如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次 D、转动转盘20次,一定有6次获得“文具盒”8. 某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图,由图可知,下列结论正确的是( )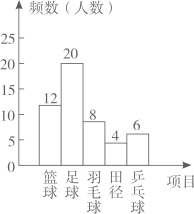 A、最喜欢篮球的人数最多 B、最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍 C、全班共有50名学生 D、最喜欢田径的人数占总人数的10%9. 如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O , 过点O作EF∥BC , EF与AB、CD分别相交于点E、F , 则△DOF的面积与△BOA的面积之比为( )
A、最喜欢篮球的人数最多 B、最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍 C、全班共有50名学生 D、最喜欢田径的人数占总人数的10%9. 如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O , 过点O作EF∥BC , EF与AB、CD分别相交于点E、F , 则△DOF的面积与△BOA的面积之比为( )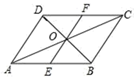 A、1:2 B、1:4 C、1:8 D、1:1610. 如图,已知一次函数y=ax+b和反比例函数y= 的图象相交于A(﹣2,y1)、B(1,y2)两点,则不等式ax+b< 的解集为( )
A、1:2 B、1:4 C、1:8 D、1:1610. 如图,已知一次函数y=ax+b和反比例函数y= 的图象相交于A(﹣2,y1)、B(1,y2)两点,则不等式ax+b< 的解集为( )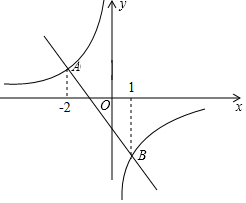 A、x<﹣2或0<x<1 B、x<﹣2 C、0<x<1 D、﹣2<x<0或x>1
A、x<﹣2或0<x<1 B、x<﹣2 C、0<x<1 D、﹣2<x<0或x>1二、填空题
-
11. 的相反数是 .12. 受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,预计某市2019年快递业务量将达到6.5亿件,数据6.5亿用科学记数法表示为13. 分解因式:8-2x2= .14. 如图,在△ABC中AB=AC , 以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D , 连接BD , 若∠A=36°,则∠CDB的大小为度.
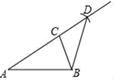 15. 某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张作纪念,全班共送了2070张相片.若全班有x名学生,根据题意,列出方程为 .16. 某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有人.
15. 某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张作纪念,全班共送了2070张相片.若全班有x名学生,根据题意,列出方程为 .16. 某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有人.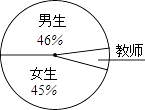 17. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是 .
17. 如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是2,则点B的横坐标是 .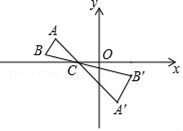 18. 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积来近似估计圆O的面积,则S= . (结果保留根号)
18. 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积来近似估计圆O的面积,则S= . (结果保留根号)三、综合题
-
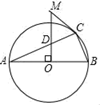
19. 计算:(π﹣ )0﹣ |﹣3|+( )﹣120. 先化简,再求值:a(a+2b)﹣(a+1)2+2a,其中 , .21. 如图所示AB是⊙O的直径,圆心为点O , 点C为⊙O上一点,OM⊥AB于点O交AC于点D , MC=MD
求证:MC为⊙O的切线.
 22. 某校举行了一次古诗词朗读竞赛,满分为10分,学生得分均为整数,成绩达到6分及6分以上为合格.达到9分或10分为优秀.这次竞赛中,甲、乙两组学生成绩统计分析表和成绩分布的折线统计图如图所示.
22. 某校举行了一次古诗词朗读竞赛,满分为10分,学生得分均为整数,成绩达到6分及6分以上为合格.达到9分或10分为优秀.这次竞赛中,甲、乙两组学生成绩统计分析表和成绩分布的折线统计图如图所示.组别
平均分
中位数
方差
合格率
优率率
甲组
6.8
a
3.76
90%
30%
乙组
b
7.5
1.96
80%
20%
 (1)、求出成绩统计分析表中a的值.(2)、小英说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察成绩统计分析表判断,小英是甲、乙哪个组的学生.(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.试写出两条支持乙组同学观点的理由.(4)、从这次参加学校古诗词朗诵竞赛的甲、乙两组成绩优秀的学生中,随机抽取两名学生参加全市古诗词朗诵竞赛,恰好是乙组学生的概率是多少?(画树状图或列表求解)23. 某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.(1)、第一批饮料进货单价多少元?(2)、若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?24. 如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据: ≈1.732, ≈1.414)
(1)、求出成绩统计分析表中a的值.(2)、小英说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察成绩统计分析表判断,小英是甲、乙哪个组的学生.(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.试写出两条支持乙组同学观点的理由.(4)、从这次参加学校古诗词朗诵竞赛的甲、乙两组成绩优秀的学生中,随机抽取两名学生参加全市古诗词朗诵竞赛,恰好是乙组学生的概率是多少?(画树状图或列表求解)23. 某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.(1)、第一批饮料进货单价多少元?(2)、若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?24. 如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据: ≈1.732, ≈1.414) 25. 如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG .
25. 如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG .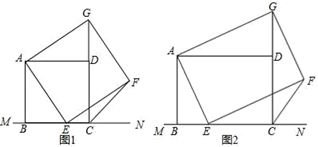 (1)、连接GD , 求证:△ADG≌△ABE;(2)、连接FC , 观察并直接写出∠FCN的度数(不要写出解答过程)(3)、如图(2),将图中正方形ABCD改为矩形ABCD , AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG , 使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.26. 如图,已知抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0).与y轴的交点为B(0,3),其顶点为C .(1)、求抛物线的解析式;(2)、将△AOB沿x轴向右平移m个长度单位(0<m<3)后得到另一个△FPE , 点A、O、B的像分别为点F、P、E .
(1)、连接GD , 求证:△ADG≌△ABE;(2)、连接FC , 观察并直接写出∠FCN的度数(不要写出解答过程)(3)、如图(2),将图中正方形ABCD改为矩形ABCD , AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG , 使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.26. 如图,已知抛物线y=﹣x2+bx+c与x轴的一个交点为A(3,0).与y轴的交点为B(0,3),其顶点为C .(1)、求抛物线的解析式;(2)、将△AOB沿x轴向右平移m个长度单位(0<m<3)后得到另一个△FPE , 点A、O、B的像分别为点F、P、E .①如图①,当点E在直线AC上时,求m的值.
②设所得的三角形△FPE与△ABC重叠部分的面积为S , 求S关于m的函数表达式.