湖南省娄底市2019年中考数学模拟试卷

试卷更新日期：2020-05-09 类型：中考模拟

进入出卷网下载

一、选择题

1. -5的绝对值是（）

A、5 B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、－5

查看试题解析
2. 下列运算正确的是（）

A、.x³•x³＝x B、（ab³）²＝ab⁶ C、x⁸÷x⁴＝x² D、（2x）³＝8x³

查看试题解析
3. 下列生态环保标志中，是中心对称图形的是 $($ $)$

A、 B、 C、 D、

查看试题解析
4. 已知组四人的成绩分别为90、60、90、60，组四人的成绩分别为70、80、80、70，用下列哪个统计知识分析区别两组成绩更恰当（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
5. 据《经济日报》2018年5月21日报道：目前，世界集成电路生产技术水平最高已达到7nm（1nm=10^﹣⁹m），主流生产线的技术水平为14～28nm，中国大陆集成电路生产技术水平最高为28nm．将28nm用科学记数法可表示为（）

A、28×10^﹣⁹m B、2.8×10^﹣⁸m C、28×10⁹m D、2.8×10⁸m

查看试题解析
6. 在下列几何体中，三视图都是圆的为（）

A、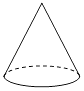 B、 C、 D、

查看试题解析
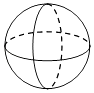7.
如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则∠ABD=（　　）

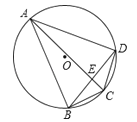A、∠ACD B、∠ADB C、∠AED D、∠ACB

查看试题解析
8. 将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′＝55°，则∠BAD′的大小是（）

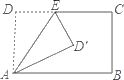A、30° B、35° C、45° D、60°

查看试题解析
9. 若关于x的一元二次方程x²+bx+c=0的两个实数根分别为x₁=﹣2，x₂=4，则b+c的值是（）

A、﹣10 B、10 C、﹣6 D、﹣1

查看试题解析
10. 已知反比例函数y= $\frac{1 - 2 m}{x}$ 的图象上有两点A（x₁ ， y₁），B（x₂ ， y₂），当x₁＜0＜x₂时，有y₁＜y₂ ，则m的取值范围是（）

A、m＜0 B、m＞0 C、m＜ $\frac{1}{2}$ D、m＞ $\frac{1}{2}$

查看试题解析
11. 程大位是我国明朝商人，珠算发明家．他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法．书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人，下列求解结果正确的是（）

A、大和尚25人，小和尚75人 B、大和尚75人，小和尚25人 C、大和尚50人，小和尚50人 D、大、小和尚各100人

查看试题解析
12. 抛物线y＝ax²+bx+c（a≠0）的对称轴为直线x＝﹣1，与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则下列结论：①4ac﹣b²＜0；②2a﹣b＝0；③a+b+c＜0；④点M（x₁ ， y₁）、N（x₂ ， y₂）在抛物线上，若x₁＜x₂ ，则y₁≤y₂ ，其中符合题意结论的个数是（）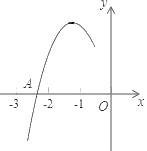

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

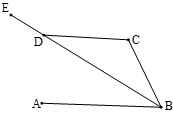
13. 函数 $y = \frac{1}{\sqrt{x - 4}}$ 中自变量x的取值范围是．

查看试题解析
14. 已知点M（3，﹣2），将它先向左平移2个单位，再向上平移4个单位后得到点N，则点N的坐标是．

查看试题解析
15. 如图，AB∥CD，BE平分∠ABC，若∠CDE=150°，则∠C=.

查看试题解析
16. 如图，正六边形ABCDEF内接于半径为3的⊙O ，则劣弧AB的长度为．

查看试题解析
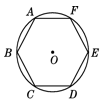17. 在﹣9，﹣6，﹣3，﹣1，2，3，6，8，11这九个数中，任取一个作为a值，能够使关于x的一元二次方程x²+ax+9＝0有两个不相等的实数根的概率是．

查看试题解析
18. 记S_n＝a₁ ， +a₂+…a_n ，令T_n＝ $\frac{S_{1} + S_{2} + ... + S_{n}}{n}$ ，则称T_n为a₁ ， a₂ ， …，a_n这列数的“凯森和”，已知a₁ ， a₂ ， …a₅₀₀的“凯森和”为2004，那么1，a₁ ， a₂ ， …a₅₀₀的“凯森和”为．

查看试题解析

三、综合题

19. 计算 $| \sqrt{3} - 1 | + 2019^{0} - {(- \frac{1}{3})}^{- 1} - 3 \tan 30^{\circ}$

查看试题解析
20. 先化简，再求值：（a﹣2b）（a+2b）﹣（a﹣2b）²+8b² ，其中a＝﹣6，b＝ $\frac{1}{3}$

查看试题解析
21. 为了加强学生课外阅读，开阔视野，某校开展了“书香校园，从我做起”的主题活动，学校随机抽取了部分学生，对他们一周的课外阅读时间进行调查，绘制出频数分布表和频数分布直方图的一部分如下：
课外阅读时间（单位：小时）
频数（人数）
频率
0＜t≤2
2
0.04
2＜t≤4
3
0.06
4＜t≤6
15
0.30
6＜t≤8
a
0.50
t＞8
5
b
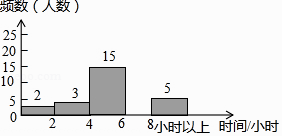
请根据图表信息回答下列问题：

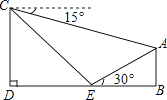
(1)、频数分布表中的a= ， b=；

(2)、将频数分布直方图补充完整；

(3)、学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”，请你估计该校2000名学生中评为“阅读之星”的有多少人？

查看试题解析
22.
如图，小丽假期在娱乐场游玩时，想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度．她先在山脚下点E处测得山顶A的仰角是30°，然后，她沿着坡度是i=1：1（即tan∠CED=1）的斜坡步行15分钟抵达C处，此时，测得A点的俯角是15°．已知小丽的步行速度是18米/分，图中点A、B、E、D、C在同一平面内，且点D、E、B在同一水平直线上．求出娱乐场地所在山坡AE的长度．（参考数据： $\sqrt{2}$ ≈1.41，结果精确到0.1米）

查看试题解析
23. 从甲市到乙市乘坐高铁列车的路程为180千米，乘坐普通列车的路程为240千米，高铁列车的平均速度是普通列车的平均速度的3倍，高铁列车的乘车时间比普通列车的乘车时间缩短了2小时．

(1)、求高铁列车的平均速度是每小时多少千米；

(2)、某日王老师要去距离甲市大约405m的某地参加14：00召开的会议，如果他买到当日10：40从甲市至该地的高铁票，而且从该地高铁站到会议地点最多需要1.5h，试问在高铁列车准点到达的情况下他能在开会之前到达吗？

查看试题解析
24. 如图，在△ABC中，∠BAC＝90°，线段AC的垂直平分线交AC于D点，交BC于E点，过点A作BC的平行线交直线ED于F点，连接AE，CF．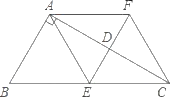

(1)、求证：四边形AECF是菱形；

(2)、若AB＝10，∠ACB＝30°，求菱形AECF的面积．

查看试题解析
25. 如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC＝PC，∠COB＝2∠PCB．

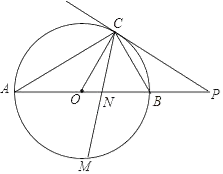(1)、求证：PC是⊙O的切线；

(2)、求证：BC＝ $\frac{1}{2}$ AB；

(3)、点M是 $\overset{⌢}{A B}$ 的中点，CM交AB于点N，若AB＝4，求MN•MC的值．

查看试题解析
26. 如图，顶点坐标为（2，﹣1）的抛物线y＝ax²+bx+c（a≠0）与y轴交于点C（0，3），与x轴交于A、B两点．

(1)、求抛物线的表达式；

(2)、设抛物线的对称轴与直线BC交于点D，连接AC、AD，求△ACD的面积；

(3)、点E为直线BC上一动点，过点E作y轴的平行线EF，与抛物线交于点F．问是否存在点E，使得以D、E、F为顶点的三角形与△BCO相似？若存在，求点E的坐标；若不存在，请说明理由．

查看试题解析

课外阅读时间（单位：小时）	频数（人数）	频率
0＜t≤2	2	0.04
2＜t≤4	3	0.06
4＜t≤6	15	0.30
6＜t≤8	a	0.50
t＞8	5	b