湖南省怀化市2019年中考数学三模试卷
试卷更新日期：2020-05-09 类型：中考模拟
一、选择题
-
1. 下列各数中是有理数的是（ ）
A、π B、0 C、 D、2. 辽宁男篮夺冠后，从4月21日至24日各类媒体关于“辽篮CBA夺冠”的相关文章达到81000篇，将数据81000用科学记数法表示为（ ）A、0.81×104 B、0.81×105 C、8.1×104 D、8.1×1053. 如图是由五个相同的小立方块搭成的几何体，这个几何体的左视图是（ ）
A、
B、
C、
D、
4. 在平面直角坐标系中，点B的坐标是（4，﹣1），点A与点B关于x轴对称，则点A的坐标是（ ）
A、（4，1） B、（﹣1，4） C、（﹣4，﹣1） D、（﹣1，﹣4）5. 下列运算不正确的是（ ）A、（m2）3=m6 B、a10÷a9=a C、x3•x5=x8 D、a4+a3=a76. 如图，AB∥CD，EF∥GH，∠1=60°，则∠2补角的度数是（ ）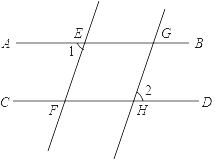
A、60° B、100° C、110° D、120°7. 下列事件中，是必然事件的是（ ）
A、任意买一张电影票，座位号是2的倍数 B、13个人中至少有两个人生肖相同 C、车辆随机到达一个路口，遇到红灯 D、明天一定会下雨8. 在平面直角坐标系中，一次函数y=kx+b的图象如图所示，则k和b的取值范围是（ ）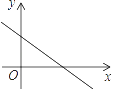
A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜09. 点A（﹣3，2）在反比例函数y= （k≠0）的图象上，则k的值是（ ）
A、﹣6 B、﹣ C、﹣1 D、610. 如图，正方形ABCD内接于⊙O，AB=2 ，则 的长是（ ）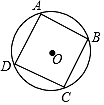
A、π B、 π C、2π D、 π二、填空题
-
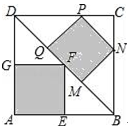
11. 不透明袋子中装有6个球，其中有1个红球、2个绿球和3个黑球，这些球除颜色外无其他差别，从袋子中随机取出1个球，则它是绿球的概率是 ．12. 若一次函数y=-2x+b（b为常数）的图象经过第二、三、四象限，则b的值可以是.（写出一个即可）13. 如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则 的值等于 ．
14. 如图，在每个小正方形的边长为1的网格中，A，E为格点，B，F为小正方形边的中点，C为AE，BF的延长线的交点．
（Ⅰ）AE的长等于；
（Ⅱ）若点P在线段AC上，点Q在线段BC上，且满足AP=PQ=QB，请在如图所示的网格中，用无刻度的直尺，画出线段PQ，并简要说明点P，Q的位置是如何找到的（不要求证明） ．
15. 如图，AC是汽车挡风玻璃前的雨刷器，如果AO=45cm，CO=5cm，当AC绕点O顺时针旋转90°时，则雨刷器AC扫过的面积为 cm2（结果保留π）．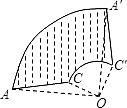
16. 如图，在⊙O中，AB为直径，CD为弦，已知∠CAB=50°，则∠ADC= ．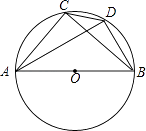
三、综合题
-
17. 先化简，再求值：（ ﹣ ）÷ ，其中a=3﹣1+2sin30°．18. 如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E．
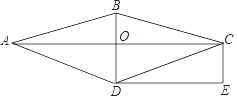(1)、求证：四边形OCED是矩形；(2)、若CE=1，DE=2，ABCD的面积是 ．19. 某学校要开展校园文化艺术节活动，为了合理编排节目，对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查（每名学生必须选择且只能选择一类），并将调查结果绘制成如下不完整统计图．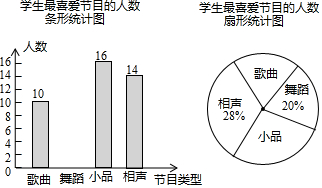
请你根据图中信息，回答下列问题：
(1)、本次共调查了名学生．
(2)、在扇形统计图中，“歌曲”所在扇形的圆心角等于度．
(3)、补全条形统计图（标注频数）．
(4)、根据以上统计分析，估计该校2000名学生中最喜爱小品的人数为人．
(5)、九年一班和九年二班各有2名学生擅长舞蹈，学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排，那么抽取的2名学生恰好来自同一个班级的概率是多少？20. 某爱心企业在政府的支持下投入资金，准备修建一批室外简易的足球场和篮球场，供市民免费使用，修建1个足球场和1个篮球场共需8.5万元，修建2个足球场和4个篮球场共需27万元．
(1)、求修建一个足球场和一个篮球场各需多少万元？(2)、该企业预计修建这样的足球场和篮球场共20个，投入资金不超过90万元，求至少可以修建多少个足球场？
21. 两栋居民楼之间的距离CD=30米，楼AC和BD均为10层，每层楼高3米．
(1)、上午某时刻，太阳光线GB与水平面的夹角为30°，此刻B楼的影子落在A楼的第几层？(2)、当太阳光线与水平面的夹角为多少度时，B楼的影子刚好落在A楼的底部．
22. 如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点．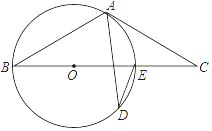
(1)、若∠ADE=25°，求∠C的度数；(2)、若AB=AC，CE=2，求⊙O半径的长．23. 在△ABC中，AB=BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．
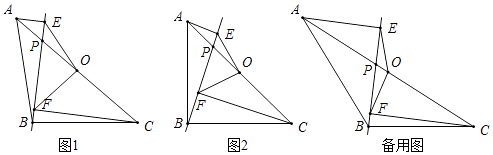(1)、如图1，请直接写出线段OE与OF的数量关系；(2)、如图2，当∠ABC=90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由(3)、若|CF﹣AE|=2，EF=2 ，当△POF为等腰三角形时，请直接写出线段OP的长．24. 如图，已知A（﹣2，0），B（4，0），抛物线y=ax2+bx﹣1过A、B两点，并与过A点的直线y=﹣ x﹣1交于点C．
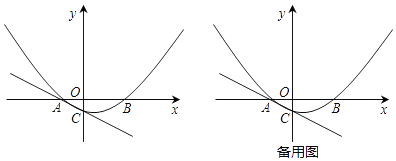(1)、求抛物线解析式及对称轴；(2)、在抛物线的对称轴上是否存在一点P，使四边形ACPO的周长最小？若存在，求出点P的坐标，若不存在，请说明理由；
(3)、点M为y轴右侧抛物线上一点，过点M作直线AC的垂线，垂足为N．问：是否存在这样的点N，使以点M、N、C为顶点的三角形与△AOC相似，若存在，求出点N的坐标，若不存在，请说明理由．